Статистические оценки
Статисти́ческие оценки
Функции от результатов наблюдений, употребляемые для статистического оценивания (См. Статистическое оценивание) неизвестных параметров распределения вероятностей изучаемых случайных величин. Например, если X1,..., Xn — независимые случайные величины, имеющие одно и то же Нормальное распределение с неизвестным средним значением а, то функции — среднее арифметическое результатов наблюдений
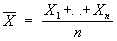
и выборочная Медиана μ = μ(X1,..., Xn) являются возможными точечными С. о. неизвестного параметра а. В качестве С. о. какого-либо параметра θ естественно выбрать функцию θ*(X1,..., Xn) от результатов наблюдений X1,..., Xn, в некотором смысле близкую к истинному значению параметра. Принимая какую-либо меру «близости» С. о. к значению оцениваемого параметра, можно сравнивать различные оценки по качеству. Обычно мерой близости оценки к истинному значению параметра служит величина среднего значения квадрата ошибки
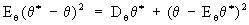
(выражающаяся через Математическое ожидание оценки E0θ* и её дисперсию (См. Дисперсия) D0θ*). В классе всех несмещённых оценок (См. Несмещённая оценка) (для которых E0θ* = 0) наилучшими с этой точки зрения будут оценки, имеющие при заданном n минимальную возможную дисперсию при всех θ. Указанная выше оценка Х для параметра а нормального распределения является наилучшей несмещенной оценкой, поскольку дисперсия любой другой несмещенной оценки а* параметра а удовлетворяет неравенству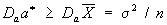 
, где σ2 — дисперсия нормального распределения. Если существует несмещенная оценка с минимальной дисперсией, то можно найти и несмещенную наилучшую оценку в классе функций, зависящих только от достаточной статистики (См. Достаточная статистика). Имея в виду построение С. о. для больших значений n, естественно предполагать, что вероятность отклонений θ* от истинного значения параметра θ, превосходящих какое-либо заданное число, будет близка к нулю при n →∞. С. о. с таким свойством называются состоятельными оценками. Несмещенные оценки, дисперсия которых стремится к нулю при n →∞, являются состоятельными. Поскольку скорость стремления к пределу играет при этом важную роль, то асимптотическое сравнение С. о. производят по отношению их асимптотической дисперсии. Так, среднее арифметическое Х в приведённом выше примере — наилучшая и, следовательно, асимптотически наилучщая оценка для параметра а, тогда как выборочная медиана μ, представляющая собой также несмещенную оценку, не является асимптотически наилучшей, т.к.
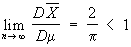
(тем не менее использование μ имеет также положительные стороны: например, если истинное распределение не является в точности нормальным, а несколько отличается от него, дисперсия Х может резко возрасти, а дисперсия μ остаётся почти той же, т. е. μ обладает свойством, называется «прочностью»). Одним из распространённых общих методов получения С. о. является метод моментов, который заключается в приравнивании определённого числа выборочных моментов к соответствующим моментам теоретического распределения, которые суть функции от неизвестных параметров, и решении полученных уравнений относительно этих параметров. Хотя метод моментов удобен в практическом отношении, однако С. о., найденные при его использовании, вообще говоря, не являются асимптотически наилучшими, Более важным с теоретической точки зрения представляется Максимального правдоподобия метод, который приводит к оценкам, при некоторых общих условиях асимптотически наилучшим. Частным случаем последнего является Наименьших квадратов метод. Метод С. о. существенно дополняется оцениванием с помощью доверительных границ (См. Доверительные границы).
Лит.: Кендалл М., Стьюарт А., Статистические выводы и связи, пер. с англ., М., 1973; Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.
А. В. Прохоров.
