Линия

I

Ли́ния (от лат. linea)

геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно.

1) В элементарной геометрии рассматриваются прямые Л., отрезки прямых, ломаные Л., составленные из отрезков, и некоторые кривые Л. Каждый вид кривых Л. определяется тем или иным специальным способом (например, окружность определяется как геометрическое место точек, имеющих заданное расстояние R от заданной точки О — центра окружности). Иногда в учебниках дают определение Л. как границы куска поверхности (поверхность определяется при этом как граница тела) или как траектории движущейся точки. Но в рамках элементарной геометрии эти определения не получают отчётливой формулировки.

2) Представление о Л. как траектории движущейся точки может быть сделано вполне строгим при помощи идеи параметрического представления Л. Например, вводя на плоскости прямоугольные координаты (x, у), можно параметрически задать окружность радиуса R с центром в начале координат уравнениями

x = R cos t, y = R sin t.

Когда параметр t пробегает отрезок 0 ≤ t ≤ 2π, точка (х, у) описывает окружность. Вообще, Л. на плоскости задают параметрическими уравнениями вида

x = φ (t), у = ψ(t),

где φ (t), ψ(t) — произвольные функции, непрерывные на каком-нибудь конечном или бесконечном интервале Δ числовой оси t. С каждым значением параметра t (из интервала Δ) уравнения (*) сопоставляют некоторую точку M, координаты которой определяются этими уравнениями. Л., заданная параметрическими уравнениями (*) есть множество точек, соответствующих всевозможным значениям t из Δ, при условии, что эти точки рассматриваются в определенном порядке, именно: если точка M₁ соответствует значению параметра t₁, а точка M₂ — значению t₂, то M₁ считается предшествующей M₂, если t₁ < t₂ При этом точки, отвечающие различным значениям параметра, всегда считаются различными.

Аналогично, в трёхмерном пространстве Л. задаётся параметрически тремя уравнениями вида

x = φ (t), у = ψ(t), z = χ (t),

где φ (t), ψ(t), χ (t) — произвольные функции, непрерывные на каком-нибудь интервале. В произвольном топологическом пространстве (См. Топологическое пространство) Т (которое, в частности, может быть плоскостью, поверхностью, обычным трёхмерным пространством, функциональным пространством и т. п.) Л. параметрически задают уравнением вида

P = φ (t),

где φ — функция действительного переменного t, непрерывная на каком-либо интервале, значения которой суть точки пространства Т. Считают, что два параметрических представления задают одну и ту же Л., если они определяют один и тот же порядок следования её точек (в смысле, указанном выше).

В анализе и топологии рассматривают обычно случай, когда область изменения параметра t есть отрезок а ≤ t ≤ b. В этом случае условие того, чтобы два параметрических представления

Р = φ (t), a ≤ t ≤ b

P = φ₁(t₁), a₁ ≤ t₁ ≤ b₁,

изображали одну и ту же Л., заключается в существовании непрерывной и строго возрастающей функции

t₁ = f(t),

для которой

f(a) = a₁, f(b) = b₁, φ (t) = φ₁[f(t)].

Такое понимание термина «Л.» наиболее естественно в большинстве вопросов анализа (например, в теории криволинейных интегралов) и механики. Так как Л. здесь рассматривается вместе с порядком, в котором пробегает её точки переменная точка М при возрастании t, то при этом естественно возникает вопрос о числе прохождений переменной точки Л. через какую-либо точку пространства. Кроме простых точек, проходимых один раз, Л. может иметь кратные точки, которые проходятся несколько раз (отвечающие различным значениям параметра).

Например, при изменении t в пределах — ∞ < t < ∞ точка с координатами

,

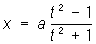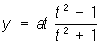
описывает строфоиду (см. рис. «Алгебраические кривые третьего порядка», № 5), попадая в положение х = 0, у = 0 два раза при t = — 1 и t = + 1.

3) Из аналитической геометрии известен и другой способ задания Л. на плоскости уравнением

F(x, y) = 0;

в пространстве — двумя уравнениями

F(x, у, z) = 0, G(x, y, z) = 0.

Ограничиваясь случаем плоскости, укажем лишь, как строится понятие алгебраической Л. (кривой) — Л., определяемой уравнением

F(x, y) = 0,

где F(x, у) — Целая алгебраическая функция, т. е. многочлен како-либо степени n ≥ 1. В этом случае считают, что два многочлена F₁(x, у) и F₂(x, у) определяют одну и ту же алгебраическую Л. в том и только в том случае, когда существует такая постоянная с ≠ 0, что выполняется тождественно соотношение

F₁(x, y) = cF₂(x, у).

Таким образом, все многочлены, определяющие одну и ту же Л., имеют одну и ту же степень n, называемую порядком соответствующей Л. Например, в аналитической геометрии принято считать, что уравнение

(х — у)² = 0

определяет Л. второго порядка, а именно, дважды взятую прямую х — у = 0.

В связи с последним примером необходимо заметить, однако, что часто целесообразно ограничиваться рассмотрением неприводимых алгебраических Л., т. е. таких Л., для которых многочлен не допускает представления F = GH, где G и Н — отличные от постоянных многочлены. Далее, в пункте 4, имеется в виду только этот случай.

Говорят, что точка (x₀, y₀) кривой F(x, у) = 0 имеет кратность m, если разложение F(x, у) по степеням ξ = х — x₀, η = у — y₀ начинается с членов степени m (по совокупности переменных ξ и η). В случае m = 2, т. е. в случае двойной точки

F(x, у) = а₁₁(х — x₀)² + 2а₁₂(х — x₀) (у — y₀) + a₂₂(y — y₀)² + ...,

где многоточие означает, что далее следуют члены высших порядков. При помощи дискриминанта

δ = a₁₁a₂₂ — а₁₂²

можно определить тип двойной точки (см. Особые точки (См. Особая точка)).

4) Часто, особенно при изучении алгебраической Л., целесообразно стать на точку зрения комплексной проективной геометрии, т. е. рассматривать, наряду с точками евклидовой действительной плоскости (или пространства), точки бесконечно удалённые и мнимые. Только при таком подходе (и надлежащем учёте кратности пересечения) становится верным, например, утверждение, что две Л. порядков n и m пересекаются в mn точках. В случае m = 1 это приводит к возможности определить порядок Л. как число n точек её пересечения с прямой.

С проективной точки зрения естественно задавать Л. на плоскости однородным уравнением

F(x₁, x₂, x₃) = 0

между однородными координатами x₁, x₂, x₃ её точек. В силу принципа двойственности с этим заданием равноправно задание Л. уравнением

Φ(ξ₁, ξ₂, ξ₃) = 0,

связывающим однородные координаты прямых, касающихся Л. Таким образом, наряду с порядком Л. (степенью уравнения F = 0) естественно возникает понятие класса Л. — степени уравнения Φ = 0. Класс алгебраических Л. можно также определить как число касательных, которые можно провести к Л. из произвольной точки. О параметрическом представлении Л. см. также Уникурсальные кривые (См. Уникурсальная кривая).

5) Рассмотренные выше (в пунктах 2—4) уточнения и обобщения понятия Л. существенно связаны с соответствующим алгебраическим и аналитическим аппаратом. В отличие от этого, современная Топология выдвинула задачу уточнения представления о Л. как о множестве точек, независимо от алгебраического или аналитического способов задания этого множества.

Если исходить из параметрического задания Л. в виде непрерывной функции P = φ (t), где t пробегает отрезок а ≤ t ≤ b, но интересоваться только полученным множеством точек без учёта порядка их следования, то приходят к понятию Л., сформулированному в 80-x гг. 19 в. К. Жорданом (см. Жордана кривая). Оказывается, что таким непрерывным образом отрезка может быть любой локально связный континуум, в частности квадрат, треугольник, куб и т. п. (см. Пеано кривая). Поэтому теперь обычно предпочитают говорить не о Л. в смысле Жордана, а о локально связных, или жордановых, континуумах. Взаимно однозначный непрерывный образ отрезка называют простой дугой, или жордановой дугой. Взаимно однозначный непрерывный образ окружности называют простой замкнутой Л. Простые дуги и простые замкнутые Л. не исчерпывают, однако, точечных множеств, заслуживающих наименования Л.

Избегая и чрезмерной общности, и чрезмерного сужения понятия Л., в современной топологии пользуются понятием Л., введённым в 1921 П. С. Урысоном, который определяет Л. (кривую) как произвольный Континуум размерности единица. Континуум имеет размерность единица, если при любом ε > 0 он может быть представлен в виде суммы конечного числа замкнутых множеств диаметра, меньшего ε, обладающих тем свойством, что никакие три из этих замкнутых множеств не имеют общей точки (см. также Размерность в геометрии). Континуум, лежащий на плоскости, будет Л. в смысле Урысона тогда и только тогда, когда он не содержит внутренних точек. Этим свойством характеризовал ранее (70-е гг. 19 в.) Л., лежащие на плоскости, Г. Кантор. Хотя определение Кантора применимо только к Л., лежащим на плоскости, иногда и общие Л. в смысле Урысона называют «канторовыми кривыми».

Л. Н. Колмогоров.

6) Ещё математики древности изучали Линии второго порядка (Эллипс, гиперболу (См. Гипербола) и параболу (См. Парабола)). Ими же был рассмотрен ряд отдельных замечательных алгебраических Л. более высокого порядка, а также некоторые трансцендентные (неалгебраические) Л. Систематическое изучение Л. и их классификация стали возможными с созданием аналитической геометрии (Р. Декарт).

Из Л. третьего порядка наиболее известны:

Декартов лист (см. рис. «Алгебраические кривые третьего порядка», № 1). уравнение в прямоугольных координатах: x³ + y³ — 3аху = 0. Впервые кривая определяется в письме Р. Декарта к П. Ферма в 1638. Полная форма кривой с наличием асимптоты, проходящей через точки ( —а, 0) и (0, —а), была определена позднее (1692) Х. Гюйгенсом и И. Бернулли. Название «декартов лист» установилось в начале 18 в.

Локон Аньези (см. рис. «Алгебраические кривые третьего порядка», № 2). Пусть имеется круг с диаметром OC = -а и отрезок BDM, построенный так, что ОВ : BD = OC : ВМ; геометрическое место точек М представляет собой локон Аньези (или верзиеру). уравнение в прямоугольных координатах: у = a³/(a² + x²). Исследование этой Л. связано с именем итальянской женщины-математика Марии Аньези (1748).

Кубическая парабола (см. рис. «Алгебраические кривые третьего порядка», № 3). уравнение в прямоугольных координатах: у = x³.

Полукубическая парабола (см. рис. «Алгебраические кривые третьего порядка», № 4), парабола Нейля. уравнение в прямоугольных координатах: у = -сх^3/2. Названа по имени английского математика У. Нейля (1657), нашедшего длину её дуги.

Строфоида (от греч. stróphos — кручёная лента и éidos — вид) (см. рис. «Алгебраические кривые третьего порядка», № 5). Пусть имеется неподвижная прямая АВ и точка С вне её на расстоянии CO = а; вокруг С вращается прямая, пересекающая АВ в переменной точке N. Если от точки N отложить по обе стороны прямой АВ отрезки NM = NM' = NO, то геометрическое место точек М и М' для всех положений вращающегося луча CN и есть строфоида. Уравнение в прямоугольных координатах: 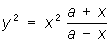; в полярных координатах: ρ = —a cos 2φ/cosφ. Впервые строфоиду исследовал Э. Торричелли (1645), название было введено в середине 19 в.

Циссоида Диоклеса (см. рис. «Алгебраические кривые третьего порядка», № 6) (греч. kissoeides, от kissós — плющ и éidos — вид), геометрическое место точек М, для которых OM = PQ (Р — произвольная точка производящего круга с диаметром а). Уравнение в прямоугольных координатах: y² = х³/(а — х); в полярных координатах: ρ = asin² φ/cos φ. Древние греки рассматривали только ту часть циссоиды, которая находится внутри производящего круга. Вместе с дугой окружности эта часть образует фигуру, напоминающую лист плюща (откуда название); наличие бесконечных ветвей было установлено в 17 в. французским математиком Ж. П. Робервалем и независимо от него бельгийским математиком Р. Ф. Слюзом.

Из Л. четвёртого и более высоких порядков наиболее известны:

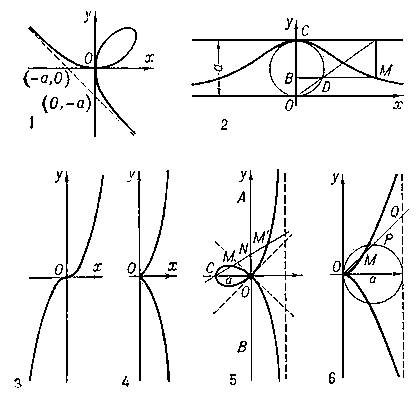
Кардиоида (от греч. kardía — сердце и éidos — вид) (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 1), кривая, описываемая какой-либо точкой М окружности радиуса а, катящейся без скольжения по неподвижной окружности того же радиуса. уравнение в прямоугольных координатах: (x² + y² — 2ах)² = 4a(x² + y²); в полярных координатах: ρ = 2а (1 + cos φ).

Конхоида Никомеда (от греч. konchoeides — похожий на раковину) (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 2), кривая, получающаяся при увеличении или уменьшении каждого радиус-вектора точек данной прямой на одну и ту же величину d, т. о., OM = OP — d или OM' = OP + d. Если расстояние от полюса О до данной прямой равно а, то уравнение в прямоугольных координатах: (х — а)²(х² + y²) — d²x² = 0, в полярных координатах: ρ = a/cosφ ± d. Впервые рассматривалась древнегреческим геометром Никомедом (около 250—150 до нашей эры), который использовал её для решения задач о трисекции угла (См. Трисекция угла) и удвоении куба (См. Удвоение куба).

Лемниската Бернулли (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 3) (от лат. lemniscatus, буквально — украшенный лентами), кривая, имеющая форму восьмёрки; геометрическое место точек, произведение расстояний которых от фокусов F₁ ( — а, 0) и F₂ (а, 0) равно а². уравнение в прямоугольных координатах: (x² + y²)² — 2a² (x² — y²) =0, в полярных координатах: ρ² = 2а² cos 2φ. Впервые рассматривалась Я. Бернулли (1694). Лемниската является частным случаем овалов Кассини и синус-спиралей.

Овалы Декарта (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 4), геометрические места точек М, расстояния которых от двух фиксированных точек F₁ и F₂, называемых фокусами, умноженные на данные числа, имеют постоянную сумму с, то есть mMF₁ + + nMF₂ = с. уравнение в прямоугольных координатах:

(x + y’’ —2rx)² — l²(x² + y²) — k = 0,

где r, l и k — некоторые постоянные, связанные с параметрами m, n и d; в полярных координатах:

(n² — m²)(² + 2((mc — n2d cos () + n²d² — с² = 0.

Помимо фокусов F₁ и F₂, имеется и третий фокус F₃, равноправный с каждым из них. При m = 1, n = 1 овал Декарта превращается в эллипс; при m = 1 и n = —1 — в гиперболу. Частным случаем овала является также улитка Паскаля. Овалы впервые исследовались Р. Декартом (1637).

Овалы Кассини (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 5), геометрические места точек М, произведение расстояний которых от двух данных точек постоянно. Пусть F₁ и F₂ точки на оси абсцисс, F₁F₂ = 2b, а произведение MF₁․MF₂ = а². уравнение в прямоугольных координатах:

(x² + y²)² — 2b² (a² — y²) = a⁴ — b⁴.

Если 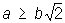, то овал Кассини — выпуклая кривая; если b < a < 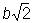, то кривая имеет вид овала с двумя утолщениями; при а = b овал Кассини превращается в лемнискату, наконец, при b > а овал Кассини является двусвязной кривой. Впервые рассмотрена Дж. Кассини (17 в.).

Улитка Паскаля (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 6), геометрическое место точек М и M', расположенных на прямых пучка (центр которого О лежит на окружности радиуса R) на расстоянии а по обе стороны от точки Р пересечения прямых с окружностью; т. о., PM = PM' = а. уравнение в прямоугольных координатах: (x² + y² — 2Rx)² — а²(х² + y²) = 0, в полярных координатах: ρ = 2R cos φ + а. При а = 2R петля стягивается в точку, в этом случае улитка Паскаля превращается в кардиоиду. Название по имени французского учёного Э. Паскаля (1588—1651), впервые изучавшего её.

Астроида (от греч. ástron — звезда и éidos — вид) (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 7), кривая, описываемая точкой подвижной окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. уравнение в прямоугольных координатах: x^2/3 + y^2/3 = а^2/3, где а — радиус неподвижной окружности. Астроида — линия 6-го порядка.

Розы (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 8), кривые, полярное уравнение которых: ρ = a sin mφ; если m — рациональное число, то розы — алгебраической Л. чётного порядка. При m нечётном роза состоит из от лепестков, при m чётном — из 2m лепестков; при m рациональном лепестки частично покрывают друг друга.

Синусоидальные спирали, синус-спирали (см. рис. «Алгебраические кривые четвертого и более высоких порядков», № 9), кривые, полярное уравнение которых ρ^m = a^m cosmφ; если m — рациональное число, то эти Л. — алгебраические. Частные случаи: m = 1 — окружность, m = — 1 — прямая, m = 2 — лемниската Бернулли, m = —2 — равнобочная гипербола, m = ¹/₂ — кардиоида, m = — ¹/₂ — парабола. При целом m > 0 Л. состоит из m лепестков, каждый из которых лежит внутри угла, равного π/m, при рациональном m > 0 лепестки могут частично покрывать друг друга; если m < 0, то Л. состоит из от бесконечных ветвей.

Большой интересный класс составляют трансцендентные Л. К ним относятся графики тригонометрических функций (См. Тригонометрические функции) (синусоида, тангенсоида), логарифмической функции (См. Логарифмическая функция), показательной функции (См. Показательная функция), гиперболических функций (См. Гиперболические функции), а также следующие Л.:

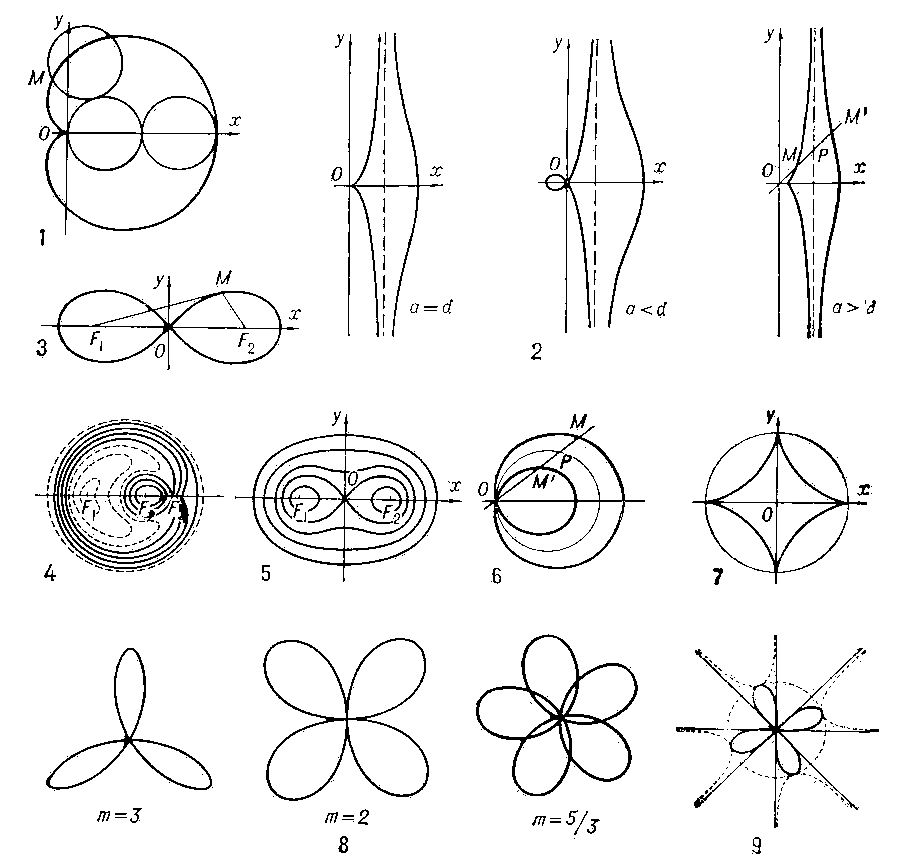
Квадратриса (см. рис. «Трансцендентные кривые», № 1). Пусть прямая MN равномерно вращается против часовой стрелки вокруг точки О, а прямая А'В' равномерно движется справа налево, оставаясь параллельной OC. Далее, пусть за время движения A'B' от AB до OC прямая MN поворачивается на прямой угол и переходит из положения OA = r в положение OC. Геометрическое место точек Р пересечения прямых MN и A'B' и есть квадратриса. уравнение в прямоугольных координатах: 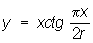; в полярных координатах: 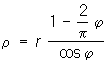. Часть квадратрисы, заключённая в квадрате OABC, была известна древнегреч. математикам. Открытие квадратрисы приписывается Гиппию Элидскому (5 в. до н. э.), использовавшему её для решения задачи о трисекции угла. Динострат (4 в. до н. э.) с помощью квадратрнсы выполнил квадратуру круга.

Трактриса (см. рис. «Трансцендентные кривые», № 2), кривая, для которой длина отрезка касательной от точки касания М до точки Р пересечения с данной прямой есть величина постоянная, равная а. Уравнение в прямоугольных координатах:

.

Цепная линия (см. рис. «Трансцендентные кривые», № 3), кривая, форму которой принимает гибкая однородная и нерастяжимая тяжёлая нить, концы которой закреплены в двух точках. уравнение в прямоугольных координатах: у = a 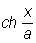= а (e^x/a + е^-х/a)/2.

Циклоида (от греч. kykloeides — кругообразный) (см. рис. «Трансцендентные кривые», № 4), кривая, которую описывает точка Р, расположенная на расстоянии а от центра круга радиуса r, катящегося без скольжения по прямой линии. Если Р лежит на окружности круга (r = а), получают обыкновенную циклоиду (см. рис. «Трансцендентные кривые», № 4а), если она лежит внутри круга (r > а), — укороченную циклоиду (см. рис. «Трансцендентные кривые», № 4б), если точка вне круга (r < а), — удлинённую циклоиду (см. рис. «Трансцендентные кривые», № 4в). Две последние Л. называют трохоидами. Уравнение в параметрической форме:

, .

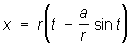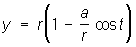Среди трансцендентных Л. особый класс составляют спирали (от греч. spéira, буквально — витое), плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь к ней или с каждым обходом удаляясь от неё. Если выбрать эту точку за полюс системы координат, то полярное уравнение спирали ρ = f(φ) таково, что f(φ + 2π) > f(φ) или f(φ + 2π) < f(φ) при всех φ. Из спиралей наиболее известны:

Архимедова спираль (см. рис. «Трансцендентные кривые», № 5), кривая, описываемая точкой, равномерно движущейся по прямой в то время, как эта прямая равномерно вращается в плоскости вокруг точки О. уравнение в полярных координатах: ρ = aφ, где а — постоянная. Эта спираль изучалась Архимедом (3 в. до н. э.) в связи с задачами трисекции угла и квадратуры круга.

Гиперболическая спираль (см. рис. «Трансцендентные кривые», № 6), кривая, описываемая точкой М, движущейся по вращающейся прямой OA, так, что её расстояние от центра вращения меняется обратно пропорционально углу поворота. Уравнение в полярных координатах: ρ = а/φ.

Жезл (см. рис. «Трансцендентные кривые», № 7), кривая, уравнение которой в полярных координатах: 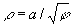. Каждому значению φ соответствуют два значения ρ — положительное и отрицательное. Кривая состоит из двух ветвей, каждая из которых асимптотически приближается к полюсу.

Логарифмическая спираль (см. рис. «Трансцендентные кривые», № 8), кривая, уравнение которой в полярных координатах: ρ = ае^кφ. Была известна многим математикам 17 в.

Спираль Корню (см. рис. «Трансцендентные кривые», № 9), клотоида, кривая, состоящая из двух ветвей, симметричных относительно начала координат. уравнение в параметрической форме:

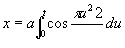, y = a .

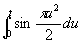Использовалась французским физиком М. А. Корню (1874) для графич. решения некоторых задач дифракции света.

Si-ci-спираль (см. рис. «Трансцендентные кривые», № 10), кривая, параметрическое уравнение которой имеет вид

,

,

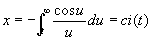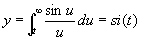si(t) и ci(t) — Интегральный синус и интегральный косинус.

К циклоиде по способу построения примыкает класс циклоидальных кривых, которые могут быть как алгебраическими, так и трансцендентными. Среди них:

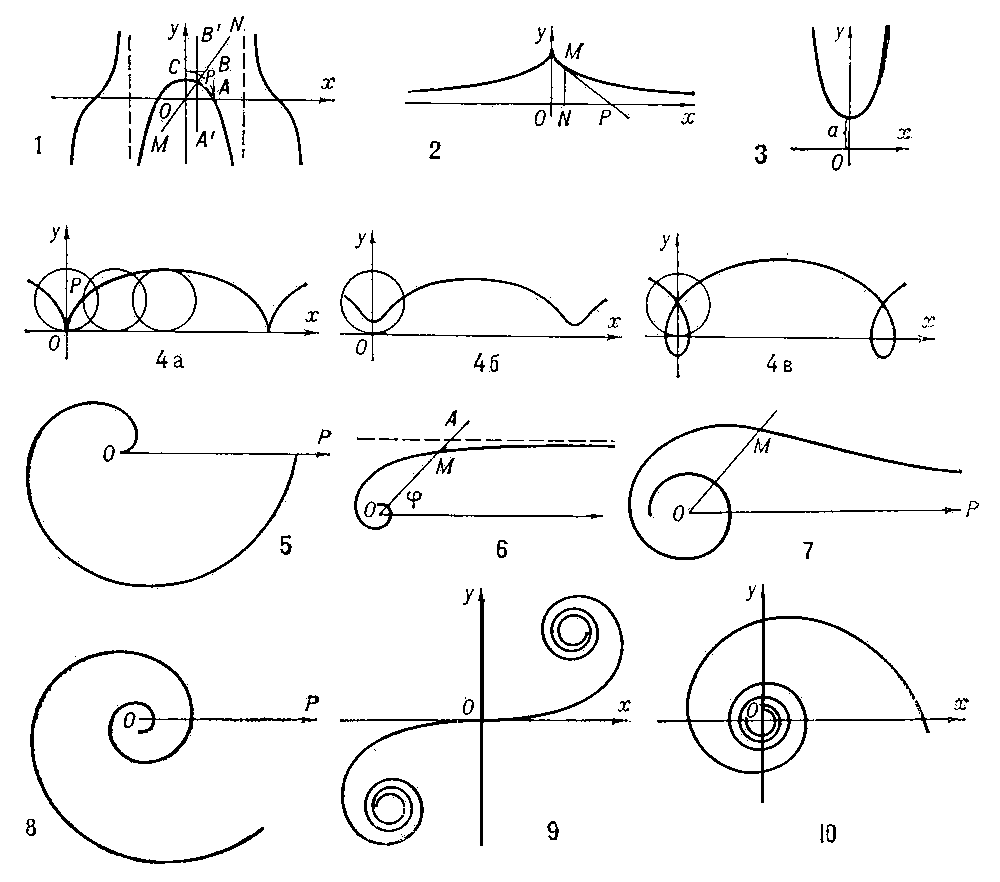
Гипоциклоида (см. рис. «Циклоидальные кривые», № 1а, 1б), кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности внутри её. Уравнение в параметрической форме:

,

,

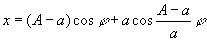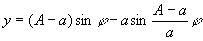где А — радиус неподвижной, а а — подвижной окружности. Вид кривой зависит от отношения А/а.

Эпициклоида (см. рис. «Циклоидальные кривые», № 2а, 2б), кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности вне её. Уравнение получится из уравнения гипоциклоиды заменой а на — а.

Удлинённая гипоциклоида (эпициклоида), кривая, описываемая точкой, лежащей вне окружности, которая катится без скольжения по другой окружности внутри (вне) её (см. рис. «Циклоидальные кривые», № 3а, 4д). Аналогично определяется укороченная гипоциклоида (эпициклоида) (см. рис. «Циклоидальные кривые», № 3б, 4б). Удлинённые и укороченные гипоциклоиды и эпициклоиды иногда называются гипо- и эпитрохоидами.

В. И. Битюцков, Ю. А. Горьков, А. Б. Иванов.

Лит.: Маркушевич А. И., Замечательные кривые, 2 изд., М. — Л., 1952; Савелов А. А., Плоские кривые. Систематика, свойства, применения (Справочное руководство), М., 1960; Пархоменко А. С., Что такое линия, М., 1954; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; Уокер А., Алгебраические кривые, пер. с англ., М., 1952; Loria G., Spezielle algebraische und transzendente ebene Kurven. Theorie und Geschichte, 2 Aufl., Bd 1—2, Lpz. — B., 1910—11.

Алгебраические кривые третьего порядка: 1 — декартов лист; 2 — локон Аньези; 3 — кубическая парабола; 4 — полукубическая парабола; 5 — строфоида; 6 — циссоида Диоклеса.

Алгебраические кривые четвёртого и более высоких порядков: 1 — кардиоида; 2 — конхоида Никомеда; 3 — лемниската Бернулли: 4 — овалы Декарта; 5 — овалы Кассини; 6 — улитка Паскаля; 7 — астроида; 8 — розы; 9 — синус-спираль.

Трансцендентные кривые: 1 — квадратриса; 2 — трактриса; 3 — цепная линия; 4 — циклоида; 5 — архимедова спираль; 6 — гиперболическая спираль; 7 — жезл; 8 — логарифмическая спираль; 9 — спираль Корню; 10 — si-ci-cпираль.

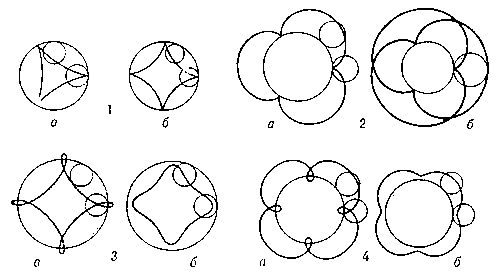
Циклоидальные кривые: 1 а, б — гипоциклоиды; 2 а, б — эпициклоиды; 3 а — удлинённая гипоциклоида; 3 б — укороченная гипоциклоида; 4а — удлинённая эпициклоида; 4б — укороченная эпициклоида.

II

Ли́ния

в генетике, размножающиеся половым путём родственные организмы, которые происходят, как правило, от одного предка или одной пары общих предков и воспроизводят в ряду поколений одни и те же наследственно устойчивые признаки. Характерные для Л. признаки искусственно поддерживаются путём отбора и близкородственного скрещивания. Различают чистые линии (См. Чистая линия) — генотипически однородное потомство самоопыляющихся растений, у которых почти все гены находятся в гомозиготном состоянии, и инбредные Л. — потомство перекрёстноопыляющегося растения, полученное путем принудительного самоопыления, или группа животных, полученная при близкородственном разведении (см. Инбридинг). Чем теснее родство родителей, тем выше степень гомозиготности (См. Гомозиготность) потомства. И в чистых, и в инбредных Л. постоянно возникающие Мутации нарушают гомозиготность. Поэтому для сохранения гомозиготности по генам, определяющим основные свойства Л., необходимо вести отбор. В животноводстве различают генеалогическую Л., т. е. группу животных, происходящую от общего предка, и заводскую Л. — однородную, качественно своеобразную, поддерживаемую отбором и подбором с использованием инбридинга группу высокопродуктивных животных, происходящую от выдающегося родоначальника и схожую с ним по конституции и продуктивности (см. Разведение по линиям). Чистые и инбредные Л. служат основой для получения высокопродуктивных гибридов в растениеводстве и животноводстве. В медико-биологических исследованиях важную роль играют Л. лабораторных животных (См. Лабораторные животные), сохраняющие константность по определённым признакам.

Лит.: Иогансен В. Л., О наследовании в популяциях и чистых линиях, пер. с нем., М. — Л., 1935; Медведев Н. Н., Практическая генетика, М., 1966.

Ю. С. Демин, Е. Я. Борисенко.