Показательная функция

Показа́тельная функция

Экспоненциальная функция, важная элементарная функция (См. Элементарные функции)

f (z) = e^z,

обозначается иногда expz; встречается в многочисленных приложениях математики к естествознанию и технике. Для любого значения z (действительного или комплексного) П. ф. определяется соотношением

;

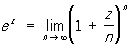Очевидно, что e⁰ = 1; при n = 1 значение П. ф. равно е — основанию натуральных логарифмов. П. ф. обладает следующими основными свойствами:

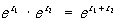и

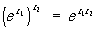
при любых значениях z₁ и z₂, кроме того, на действительной оси (рис.) П. ф. e^x > 0 и при n → ∞ возрастает быстрее любой степени х, а при х → - ∞ убывает быстрее любой степени 1/x:

, ,

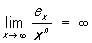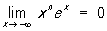каков бы ни был показатель n. Функцией, обратной по отношению к П. ф., является Логарифмическая функция: если ω = e^z, то z = lnω.

Рассматривается также П. ф. a^z при основаниях а > 0, отличных от е [например, в школьном курсе математики для действительных значений z = х рассматриваются П. ф. 2^x, (¹/₂) ^x и т.д.]. П. ф. a^z связана с П. ф. e^z (основной) соотношением

a^z = e^zlna.

П. ф. e^x является целой трансцендентной функцией (См. Трансцендентные функции). Она допускает следующее разложение в степенной ряд:

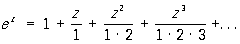, (1)

сходящийся во всей плоскости z. Равенство (1) также может служить определением П. ф.

Полагая z = х + iy, Л. Эйлер получил (1748) формулу:

e^z = e^x+iy = e^x (cosy + isiny), (2)

связывающую П. ф. с тригонометрическими функциями (См. Тригонометрические функции). Из неё вытекают соотношения:

, .

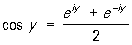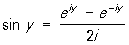Функции

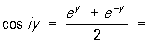ch y, 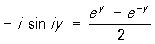= sh y

называются гиперболическими функциями (См. Гиперболические функции), обладают рядом свойств, сходных со свойствами тригонометрических функций, и играют наряду с последними важную роль в различных приложениях математики.

Из соотношения (2) следует, что П. ф. (комплексного переменного z) имеет период 2πi, то есть e^z+2πi = e^z или e^2πi = 1. Производная П. ф. равна самой функции: (e^z)' = e^z.

Указанными свойствами П. ф. определяются её многочисленные приложения. В частности, П. ф. выражает закон (т. н. закон естественного роста), определяющий течение процессов, скорость которых пропорциональна наличному значению изменяющейся величины; примером могут служить химические мономолекулярные реакции или, при известных условиях, рост колоний бактерий. Периодичность П. ф. комплексного переменного наряду с другими её свойствами является причиной, по которой эта функция играет исключительно важную роль при изучении всяких периодических процессов, в частности колебаний и распространения волн.

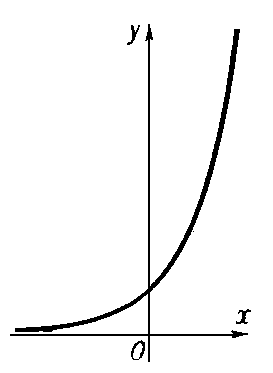
Рис. к ст. Показательная функция.