Подстановка

Подстано́вка

Элементов данного множества (математическая), замена каждого из его элементов а каким-либо другим элементом φ(а) из того же множества; при этом должны получаться все элементы исходного множества и каждый только один раз. Таким образом, понятие П. по существу совпадает с понятием взаимно однозначного отображения множества на себя (см. Взаимно однозначное соответствие), однако оно применяется большей частью к конечным множествам. Только этот случай и рассматривается ниже. Для П. принята запись

,

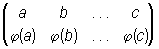здесь под каждым из элементов данного множества написан соответствующий ему элемент. Так как свойства П. не зависят от природы элементов а, b,..., с, то большей частью (во всяком случае — в учебных целях) используют целые числа 1, 2,..., n, при этом в верхней строке они преимущественно записываются в своём естественном порядке; П. принимает вид

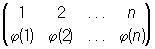
или проще

,

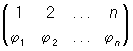где φ₁, φ₂,..., φ_n — те же числа 1, 2,..., n, но записанные, возможно, в каком-либо ином порядке. Т. о., вторая строка П. образует перестановку (См. Перестановка) φ₁, φ₂,..., φ_n из чисел 1, 2,..., n. Различных П. из n элементов существует столько же, сколько и перестановок, т.е. n! = 1․2․3․...․n. Подстановка

,

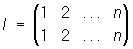оставляющая на месте все элементы, называется единичной, или тождественной. Для каждой подстановки А существует обратная, т. е. такая, которая переводит φ_i в i; она обозначается через А^-1. Например,

;

.

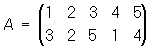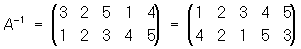Результат последовательного применения двух подстановок А и В снова будет некоторой подстановкой С: если А переводит i в φ_i, а В переводит φ_i в ψ_i, то С переводит i в ψ_i. Подстановка С называется произведением подстановок А и В, что записывается так: С = АВ. Например, если

; ,

.

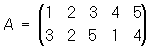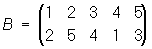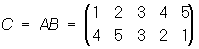При умножении П. не выполняется закон коммутативности, т. е., вообще говоря, АВ ≠ ВА; так, в том же примере

.

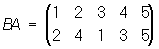Легко видеть, что IA = AI = А, АА^-1= А^-1А = I, А (ВС) = (АВ) С (ассоциативный закон). Т. о., все П. из n элементов образуют группу (См. Группа), называемую симметрической группой (См. Симметрическая группа) степени n.

П., переставляющая местами только 2 элемента i и j, называют транспозицией и обозначается так: (i, j), например

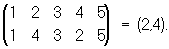
Любую П. можно разложить в произведение транспозиций. Число множителей при разложении разными способами данной П. в произведение транспозиций всегда будет либо чётным, либо нечётным. В соответствии с этим и П. называют либо чётной, либо нечётной; например, А = (1, 3)(5, 4)(5, 1) — нечётная П. Чётность П. можно определить также по числу инверсий, т. е. по числу нарушений порядка в нижней строке П., если числа верхней строки расположены в их естественном порядке: чётность П. совпадает с чётностью числа инверсий; например, в нижней строке подстановки А имеется 5 инверсий, т. е. случаев, когда большее число стоит раньше меньшего: (3, 2), (3, 1),(2, 1), (5, 1) и (5, 4). Существует n!/2 чётных и n!/2 нечётных П. из n элементов.

П., циклически переставляющая данную группу элементов, а остальные элементы оставляющая на месте, называется циклом. Число переставляемых элементов называют длиной цикла. Например, подстановка А есть цикл длины 4: она переводит 1 в 3, 3 в 5, 5 в 4, 4 в1; коротко это записывается так: А = (1, 3, 5, 4). Транспозиция есть цикл длины 2. Любую П. можно разложить в произведение независимых (т. е. не имеющих общих элементов) циклов. Например,

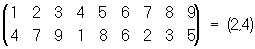
Термин «П.» в интегральном исчислении (См. Интегральное исчисление) означает замену переменной в подынтегральной функции.

Лит.: Курош А. Г., Курс высшей алгебры, 10 изд., М. — Л., 1971.