Группа

I

Гру́ппа

одно из основных понятий современной математики. Теория Г. изучает в самой общей форме свойства действий, наиболее часто встречающихся в математике и её приложениях (примеры таких действий — умножение чисел, сложение векторов, последовательное выполнение преобразований и т. п.). Общность теории Г., а вместе с тем и широта её приложений обеспечиваются тем, что она изучает свойства действий в их чистом виде, отвлекаясь как от природы элементов, над которыми выполняется действие, так и от природы самого действия. В то же время теория Г. изучает не совсем произвольные действия, а лишь те, которые обладают рядом основных свойств, перечисляемых в определении Г. (см. ниже).

К понятию Г. можно прийти, например, исследуя симметрию геометрических фигур. Так, квадрат (рис. a) представляется симметричной фигурой, так как, например, его поворот j около центра на 90° по часовой стрелке или Зеркальное отражение y относительно диагонали AC не изменяют его положения; всего существует 8 различных движений (См. Движение), совмещающих квадрат с собой. Для круга (рис. б) таких движений, очевидно, уже бесконечно много — таковы, например, все его повороты около центра. А для фигуры, изображенной на рис. в, существует лишь одно движение, совмещающее её с собой, — тождественное, т. е. оставляющее каждую точку фигуры на месте.

Множество G различных движений, самосовмещающих данную фигуру, и служит характеристикой большей или меньшей её симметричности: чем больше множество G, тем симметричнее фигура. Определим на множестве G композицию, т.е. действие над элементами из G, по следующему правилу: если j,y — два движения из G, то результатом их композиции (иногда говорят «произведением» j и y) называется движение jοy, равносильное последовательному выполнению сначала движения j , а затем движения y. Например, если j, y — движения квадрата, указанные выше, то φοψ — отражение квадрата относительно оси, проходящей через середины сторон AB и CD. Множество движений G, взятое с определённой на нём композицией, называется группой симметрии данной фигуры. Очевидно, композиция на множестве G удовлетворяет следующим условиям: 1) (φ○ψ)○θ = φ○ (ψ○θ) для любых φ, ψ, θ из G; 2) в G существует такой элемент ε, что ε○φ = φ○ε = φ для любого φ из G; 3) для любого φ из G существует в G такой элемент φ^-1, что φ○φ^-1 =

φ^-1○φ = ε. Действительно, в качестве ε можно взять тождественное движение, а в качестве φ^-1 — движение, обратное φ, т. е. возвращающее каждую точку фигуры из нового положения в старое.

Общее (формальное) определение Г. таково. Пусть G — произвольное множество каких-нибудь элементов, на котором задана композиция (иначе: действие над элементами): для любых двух элементов φ,ψ из G определён некоторый элемент φοψ снова из G. Если при этом выполняются условия 1), 2), 3), то множество G с заданной на нём композицией называется группой.

Например, если G — множество всех целых чисел, а композиция на G — их обычное сложение (роль ε будет играть число 0, а роль (φ^-1 — число —φ), то G — группа. Часть Н множества G, состоящая из чётных чисел, сама будет Г. относительно той же композиции. В таких случаях говорят, что Н — подгруппа группы G. Отметим, что обе эти Г. удовлетворяют следующему дополнительному условию: 4) φ○ψ = ψ○φ для любых φ, ψ из группы. Всякая группа с этим условием называется коммутативной, или абелевой.

Ещё один пример группы. Подстановкой множества символов 1, 2, ..., n называется таблица

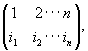
где в нижней строчке стоят те же символы 1, 2, ..., n, но, вообще говоря, в другом порядке. Композицию двух подстановок φ,ψ определяют следующим правилом: если под символом х в подстановке φ стоит символ у, а под символом у в подстановке ψ стоит символ z, то в подстановке φ○ψ под символом х ставится символ z. Например,

○

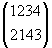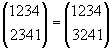
Можно проверить, что множество подстановок n символов относительно такой композиции является группой. При n ≥ 3 она неабелева.

Историческая справка. Понятие Г. послужило во многих отношениях образцом при перестройке алгебры и вообще математики на рубеже 19—20 вв. Истоки понятия Г. обнаруживаются в нескольких дисциплинах, главная из которых — теория решений алгебраических уравнений в радикалах. В 1771 французские математики Ж. Лагранж и А.Вандермонд впервые для нужд этой теории применили подстановки (для теории Г. особенно важен «Мемуар об алгебраическом решении уравнений» Лагранжа). Затем в ряде работ итальянского математика П. Руффини (1799 и позднее), посвященных доказательству неразрешимости уравнения 5-й степени в радикалах, систематически используется замкнутость множества подстановок относительно их композиции и по существу описаны подгруппы группы всех подстановок пяти символов. Глубокие связи между свойствами Г. подстановок и свойствами уравнений были указаны норвежским математиком Н. Абелем (1824) и французским математиком Э. Галуа (1830). Галуа принадлежат и конкретные достижения в теории Г.: открытие роли т. н. нормальных подгрупп в связи с задачей о разрешимости уравнений в радикалах, установление свойства простоты знакопеременных Г. степени n ≥ 5 и др.; он же ввёл термин «группа» (le Group), хотя и не дал строгого определения. Важную роль в систематизации и развитии теории Г. сыграл трактат французского математика К. Жордана о Г. подстановок (1870).

Независимо и из других соображений идея Г. возникла в геометрии, когда в середине 19 в. на смену единой античной геометрии пришли многочисленные «геометрии» и остро встал вопрос об установлении связей и родства между ними. Выход из создавшегося положения был намечен исследованиями по проективной геометрии, посвященными изучению поведения фигур при различных преобразованиях. Постепенно интерес в этих исследованиях перешёл на изучение самих преобразований и поиск их классификации. Таким «изучением геометрического родства» много занимался немецкий математик А. Мёбиус. Заключительным этапом на этом пути явилась «Эрлангенская программа» немецкого математика Ф. Клейна (1872), положившая в основу классификации геометрий понятие Г. преобразований: каждая геометрия определена некоторой Г. преобразований пространства, и только те свойства фигур принадлежат к данной геометрии, которые инвариантны относительно преобразований соответствующей Г.

Третий источник понятия Г. — теория чисел. Уже Л. Эйлер (1761), изучая «вычеты, остающиеся при делении степеней», по существу пользовался сравнениями и разбиениями на классы вычетов, что на теоретико-групповом языке означает разложение Г. на смежные классы по подгруппе. К. Гаусс в «Арифметических исследованиях» (1801), занимаясь уравнением деления круга, фактически определил подгруппы его группы Галуа. Там же, изучая «композицию двоичных квадратичных форм», Гаусс по существу доказывает, что классы эквивалентных форм образуют относительно композиции конечную абелеву Г.. Развивая эти идеи, немецкий математик Л. Кронекер (1870) вплотную подошёл к основным теореме о конечных абелевых Г., хотя и не сформулировал её явно.

Осознание в конце 19 в. принципиального единства теоретико-групповых форм мышления, существовавших к тому времени независимо в разных областях математики, привело к выработке современного абстрактного понятия Г. (норвежский математик С. Ли, нем. математик Ф. Фробениус и др.). Так, уже в 1895 Ли определял Г. как совокупность преобразований, замкнутую относительно их композиции, удовлетворяющей условиям 1), 2), 3). Изучение Г. без предположения их конечности и без каких бы то ни было предположений о природе элементов впервые оформилось в самостоятельную область математики с выходом книги О. Ю. Шмидта «Абстрактная теория групп» (1916).

Теория групп. Конечной целью собственно теории Г. является описание всех возможных групповых композиций. Теория Г. распадается на ряд больших разделов, выделяемых чаще всего дополнительными условиями на групповую композицию или внесением в Г. дополнительных структур, связанных определённым образом с групповой композицией. Перечислим важнейшие разделы теории групп.

а) Теория конечных Г. Основная проблема этой старейшей ветви теории Г. — классификация т. н. простых конечных Г., играющих роль кирпичей при построении произвольной конечной Г. Одним из наиболее глубоких фактов, установленных в этой теории, является теорема о том, что всякая неабелева простая конечная Г. состоит из чётного числа элементов.

б) Теория абелевых Г. Отправной точкой многих исследований в этой области служит основная теорема о конечно-порождённых абелевых Г., полностью выясняющая их строение.

в) Теория разрешимых и нильпотентных Г. Понятие разрешимой Г. является обобщением понятия абелевой Г. Оно по существу идёт от Галуа и тесно связано с разрешимостью уравнений в радикалах. Для конечных Г. это понятие может быть определено многими равносильными способами, которые перестают быть равносильными при отказе от конечности Г. Изучение возникающих при этом классов Г. составляет предмет теории обобщённо разрешимых и обобщённо нильпотентных Г.

г) Теория Г. преобразований. Понятие Г. возникло исторически именно как понятие Г. преобразований, но в дальнейшем было освобождено от этой конкретной оболочки. Тем не менее теория Г. преобразований осталась важной частью общей теории. Типичный вопрос в ней: какими абстрактными свойствами обладает Г., заданная как Г. преобразований некоторого множества? Особое внимание привлекают, в частности, Г. подстановок и Г. матриц.

д) Теория представлений Г. — важное орудие изучения абстрактных Г. Представление абстрактной Г. в виде некоторой конкретной Г. (например, в виде Г. подстановок или матриц) позволяет проводить тонкие вычисления и с их помощью обнаруживать важные абстрактные свойства. Особенно велики успехи теории представлений в теории конечных Г., где с её помощью получен ряд результатов, недоступных пока абстрактным методам.

е) Из разделов теории групп, выделяемых внесением в Г. дополнительных структур, согласованных с групповой композицией, отметим теорию топологических Г. (в них групповая композиция в некотором смысле непрерывна), в частности её старейшую ветвь — теорию групп Ли.

Теория Г. является одной из самых развитых областей алгебры и имеет многочисленные применения как в самой математике, так и за её пределами. Например, с помощью теории Г. русский учёный Е. С. Федоров (1890) решил задачу классификации правильных пространственных систем точек, являющуюся одной из основных задач кристаллографии. Это был исторически первый случай применения теории Г. непосредственно в естествознании. Большую роль играет теория Г. в физике, например в квантовой механике, где широко используются соображения симметрии и теория представлений Г. линейными преобразованиями.

Лит.: Александров П. С., Введение в теорию групп, 2 изд., М., 1951; Мальцев А. И., Группы и другие алгебраические системы, в кн.: Математика, ее содержание, методы и значение, т. 3, М., 1956, с. 248—331; Курош А. Г., Теория групп, 3 изд., М., 1967; Холл М., Теория групп, пер. с англ., М., 1962; Варден Б. Л. ван дер. Метод теории групп в квантовой механике, пер. с нем., Хар.,1938; Шмидт О. Ю., Абстрактная теория групп, в кн.: Шмидт О. Ю. Избр. труды. Математика, М., 1959; Федоров Е. С., Симметрия правильных систем фигур, в кн.: Федоров Е.С., Симметрия и структура кристаллов. Основные работы, М., 1949; WussinG Н., Die Genesis des abstrakten GruppenbeGriffes B.1969 S.1

М. И. Каргаполов, Ю. И. Мерзляков.

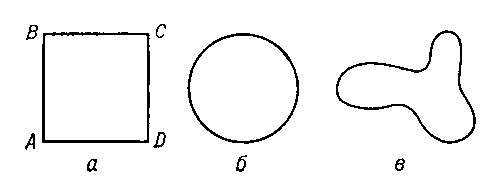
Рис. к ст. Группа.

II

Гру́ппа (нем. Gruppe)

(военное), 1) объединение соединений и частей под общим командованием старшего начальника для выполнения оперативной (боевой) задачи. В ход Великой Отечественной войны 1941—45 в Советских Вооруженных Силах создавались оперативные Г., выполнявшие задачи во фронтовой наступательной или оборонительной операции обычно в отрыве от главных сил, и подвижные Г. для развития наступления в глубине обороны противника после её прорыва. Для обеспечения боевых действий создавались артиллерийские (миномётные) и зенитно-артиллерийские Г. 2) В 30-х гг. 20 в.- часть боевого порядка соединений сов. сухопутных войск который делился на ударную сковывающую и огневую Г. 3) Штатная организация а) в вооруженых силах США: Г. армейской авиации, Г. войск специального назначения (для ведения диверсионно-подрывных действий на территории противника); 6) в вооруженных силах Великобритании: пехотная бригадная Г. общевойсковое тактическое соединение.

III

Гру́ппа (геологическое)

подразделение общей стратиграфической шкалы, объединяющее комплекс пород, образовавшихся в течение одной геологической эры. Термин «Г.» был принят на 2-й сессии Геологического международного конгресса в 1801. Американские геологи, оспаривая это решение, применяют вместо Г. термин эратема, а Г. называют подразделение местной стратиграфической шкалы. Г. подразделяются на системы; несколько Г. составляют эоно — тему. Каждая Г. соответствует определенному этапу развития Земли и земной коры, характеризуется своеобразием геологических отложений и ископаемых организмов, Различают пять Г.: архейскую, протерозойскую, палеозойскую, мезозойскую и кайнозойскую.

Б.М. Келлер.