энтропия
ЭНТРОПИЯ
функция состояния S термодинамич. системы, изменение которой dS для бесконечно малого обратимого изменения состояния системы равно отношению количества теплоты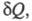 полученного системой в этом процессе (или отнятого от системы), к абс. температуре Т:
полученного системой в этом процессе (или отнятого от системы), к абс. температуре Т:
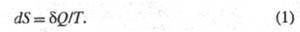
Величина dS является полным дифференциалом, т. е. ее интегрирование по любому произвольно выбранному пути дает разность между значениями Э. в начальном (А) и конечном (В) состояниях:
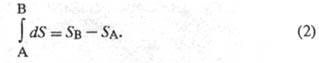
Теплота не является функцией состояния, поэтому интеграл от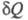 зависит от выбранного пути перехода между состояниями А и В.
зависит от выбранного пути перехода между состояниями А и В.
Э. измеряется в Дж/(моль-град).
Понятие Э. как функции состояния системы постулируется вторым началом термодинамики, которое выражает через Э. различие между необратимыми и обратимыми процессами: для первых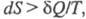 для вторых
для вторых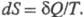
Э. как функция внутренней энергии U системы, объема V и числа молей ni i-го компонента представляет собой характеристич. функцию (см. термодинамические потенциалы). Это является следствием первого и второго начал термодинамики и записывается уравнением:
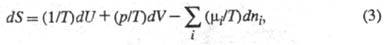
где р — давление; 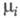 - хим. потенциал i-го компонента. Производные Э. по естеств. переменным U, V и ni равны:
- хим. потенциал i-го компонента. Производные Э. по естеств. переменным U, V и ni равны:
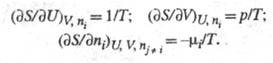
Простые формулы связывают Э. с теплоемкостями при пост. давлении Cр и пост, объеме Cv:
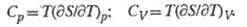
С помощью Э. формулируются условия достижения термодинамич. равновесия системы при постоянстве ее внутр. энергии, объема и числа молей i-го компонента (изолир. система) и условие устойчивости такого равновесия:
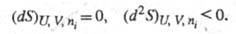
Это означает, что Э. изолир. системы достигает максимума в состоянии термодинамич. равновесия. Самопроизвольные процессы в системе могут протекать только в направлении возрастания Э.
Э. относится к группе термодинамич. функций, называемых функциями Массье-Планка. Другие функции, принадлежащие к этой группе — функция Массье Ф1 = S — (1/T)U и функция Планка Ф2 = S — (1/T)U — (p/T)V, м. б. получены в результате применения к Э. преобразования Лежандра.
Согласно третьему началу термодинамики (см. тепловая теорема), изменение Э. в обратимой хим. реакции между веществами в конденсир. состоянии, стремится к нулю при T → 0:
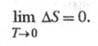
Постулат Планка (альтернативная формулировка тепловой теоремы) устанавливает, что Э. любого хим. соед. в конденсир. состоянии при абс. нуле температуры является условно нулевой и м. б. принята за начало отсчета при определении абс. значения Э. вещества при любой температуре. Уравнения (1) и (2) определяют Э. с точностью до постоянного слагаемого.
В хим. термодинамике широко используют след. понятия: стандартная Э. 5ю, т. е. Э. при давлении р=1,01∙105 Па (1 атм); стандартная Э. хим. реакции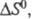 т. е. разница стандартных Э. продуктов и реагентов; парциальная молярная Э. компонента многокомпонентной системы
т. е. разница стандартных Э. продуктов и реагентов; парциальная молярная Э. компонента многокомпонентной системы
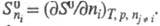
Для расчета хим. равновесий применяют формулу:
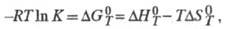
где К — константа равновесия; 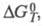
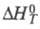 и
и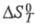 - соотв. стандартные энергия Гиббса, энтальпия и энтропия реакции; R -газовая постоянная.
- соотв. стандартные энергия Гиббса, энтальпия и энтропия реакции; R -газовая постоянная.
Определение понятия Э. для неравновесной системы опирается на представление о локальном термодинамич. равновесии. Локальное равновесие подразумевает выполнение уравнения (3) для малых объемов неравновесной в целом системы (см. термодинамика необратимых процессов). При необратимых процессах в системе может осуществляться производство (возникновение) Э. Полный дифференциал Э. определяется в этом случае неравенством Карно-Клаузиуса:
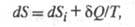
где dSi > 0 — дифференциал Э., не связанный с потоком тепла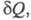 а обусловленный производством Э. за счет необратимых процессов в системе (диффузии, теплопроводности, хим. реакций и т. п.). Локальное производство Э.
а обусловленный производством Э. за счет необратимых процессов в системе (диффузии, теплопроводности, хим. реакций и т. п.). Локальное производство Э.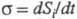 (t — время) представляется в виде суммы произведений обобщенных термодинамич. сил Xi на обобщенные термодинамич. потоки Ji:
(t — время) представляется в виде суммы произведений обобщенных термодинамич. сил Xi на обобщенные термодинамич. потоки Ji:
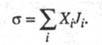
Производство Э. за счет, напр., диффузии компонента i обусловлено силой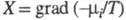 и потоком вещества J; производство Э. за счет хим. реакции- силой Х=А/Т, где А-химическое сродство, и потоком J, равным скорости реакции. В статистич. термодинамике Э. изолир. системы определяется соотношением:
и потоком вещества J; производство Э. за счет хим. реакции- силой Х=А/Т, где А-химическое сродство, и потоком J, равным скорости реакции. В статистич. термодинамике Э. изолир. системы определяется соотношением: 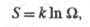 где k — постоянная Больцмана;
где k — постоянная Больцмана; 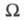 - термодинамич. вес состояния, равный числу возможных квантовых состояний системы с заданными значениями энергии, объема, числа частиц. Равновесное состояние системы отвечает равенству заселенностей единичных (невырожденных) квантовых состояний. Возрастание Э. при необратимых процессах связано с установлением более вероятного распределения заданной энергии системы по отд. подсистемам. Обобщенное статистич. определение Э., относящееся и к неизолир. системам, связывает Э. с вероятностями разл. микросостояний след. образом:
- термодинамич. вес состояния, равный числу возможных квантовых состояний системы с заданными значениями энергии, объема, числа частиц. Равновесное состояние системы отвечает равенству заселенностей единичных (невырожденных) квантовых состояний. Возрастание Э. при необратимых процессах связано с установлением более вероятного распределения заданной энергии системы по отд. подсистемам. Обобщенное статистич. определение Э., относящееся и к неизолир. системам, связывает Э. с вероятностями разл. микросостояний след. образом:
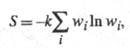
где wi — вероятность i-го состояния.
Абсолютную Э. хим. соед. определяют экспериментально, гл. обр. калориметрич. методом, исходя из соотношения:
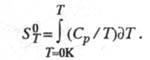
Использование второго начала позволяет определять Э. хим. реакций по эксперим. данным (метод электродвижущих сил, метод давления пара и др.). Возможен расчет Э. хим. соед. методами статистич. термодинамики, исходя из мол. постоянных, мол. массы, геометрии молекулы, частоты нормальных колебаний. Такой подход успешно осуществляется для идеальных газов. Для конденсир. фаз статистич. расчет дает значительно меньшую точность и проводится в ограниченном числе случаев; в последние годы в этой области достигнуты значит. успехи.
Э. хим. соед. табулированы в справочниках. Как правило, для конденсир. фаз приводят результаты калориметрич. измерений, для газообразных — статистич. расчета.
Первая мат. формулировка второго начала термодинамики принадлежит Р. Клаузиусу (1854), который ввел понятие Э. в 1865; связь Э. с вероятностью состояния системы впервые была установлена Л. Больцманом в 1872.
Лит. см. при ст. химическая термодинамика.
М. В. Коробов
Значения в других словарях
- Энтропия — (от греч. entropía — поворот, превращение) понятие, впервые введенное в термодинамике (См. Термодинамика) для определения меры необратимого рассеяния энергии. Э. широко применяется и в других областях науки: в статистической физике (См. Большая советская энциклопедия
- энтропия — -и, ж. 1. физ. Одна из величин, характеризующих тепловое состояние тела или системы тел; мера внутренней неупорядоченности системы. 2. В теории информации — мера неопределенности какого-л. опыта, который может иметь разные исходы. [От греч. ’εν — в, на и τροπή — поворот, превращение] Малый академический словарь
- Энтропия — Теоретико-информационная мера степени неопределенности случайной величины. Если — дискретная случайная величина, определенная на нек-ром вероятностном пространстве и принимающая значения x1, x2, . . . с распределением вероятностей... Математическая энциклопедия
- ЭНТРОПИЯ — (от греч. entropia — поворот, превращение), понятие, впервые введённое в термодинамике для определения меры необратимого рассеяния энергии. Э. широко применяется и в др. областях науки: в статистической физике как мера вероятности осуществления к.-л. Физический энциклопедический словарь
- ЭНТРОПИЯ — ЭНТРОПИЯ (от греч. entropia — поворот, превраи^ение) — англ. entropy; нем. Entropie. 1. Мера внутренней неупорядоченности системы. 2. В кибернетике и теории вероятностей — меране-определенности случайной величины. Социологический словарь
- энтропия — орф. энтропия, -и Орфографический словарь Лопатина
- энтропия — Эн/троп/и́/я [й/а]. Морфемно-орфографический словарь
- энтропия — В теории информации — мера неопределенности состояния объекта; мера неопределенности некоторой ситуации (случайной величины) с конечным или счетным числом исходов. Толковый переводоведческий словарь / Л.Л. Нелюбин. — 3-е изд., перераб. — М.: Флинта: Наука, 2003 Толковый переводоведческий словарь
- энтропия — ЭНТРОПИЯ и, ж. entropie f., нем. Entropie <�гр. en в, внутрь + trope поворот, превращение. 1. Физическая величина, характеризующая тепловое состояние тела или системы тел и возможные изменения этих состояний. Вычисление энтропии. БАС-1. Словарь галлицизмов русского языка
- энтропия — ЭНТРОПИЯ (от греч. in — в и trope — поворот, превращение) — понятие классической термодинамики, введенное Р. Клаузиусом. С его помощью формулируется один из ее основных законов, утверждающий, что Э. в замкнутой системе не может убывать. Когда... Энциклопедия эпистемологии и философии науки
- ЭНТРОПИЯ — ЭНТРОПИЯ, показатель случайности или неупорядоченности строения физической системы. В ТЕРМОДИНАМИКЕ энтропия выражает количество тепловой энергии, пригодной для совершения работы: чем энергии меньше, тем выше энтропия. Научно-технический словарь
- ЭНТРОПИЯ — ЭНТРОПИЯ (греч en — в, tropia — поворот, превращение) — понятие классической физики (введено в науку Р. Клаузиусом в 19 в.), посредством которого, в частности, описывалось действие второго начала термодинамики: в замкнутой системе... Новейший философский словарь
- энтропия — ЭНТРОПИЯ -и; ж. [от греч. en — в, на и tropos — поворот, направление] 1. Физ. Одна из величин, характеризующих тепловое состояние тела или системы тел; мера внутренней неупорядоченности системы. 2. Спец. Мера неопределённости какого-л. опыта, который может иметь разные исходы. Толковый словарь Кузнецова
- ЭНТРОПИЯ — ЭНТРОПИЯ (от греч. entropia — поворот, превращение) (обычно обозначается S) — функция состояния термодинамической системы, изменение которой dS в равновесном процессе равно отношению количества теплоты dQ, сообщенного системе или отведенного от нее... Большой энциклопедический словарь
- энтропия — [гр. в + поворот, превращение] – 1) физ. особая физическая величина; характеризует в обычно наблюдаемых нами явлениях и процессах рассеяние, обесценение энергии... Большой словарь иностранных слов
- ЭНТРОПИЯ — (от греч. entropia — поворот, превращение) в теории информации: величина, характеризующая степень неопределенности системы. Экономический словарь терминов
- энтропия — энтропия I ж. Физическая величина, характеризующая тепловое состояние тела или системы тел и возможные изменения этих состояний; мера внутренней неупорядоченности систем (в термодинамике). II ж. Мера неопределённости какого-либо опыта, который может иметь разные исходы. Толковый словарь Ефремовой
- Энтропия — См. Термохимия и Теплота. Энциклопедический словарь Брокгауза и Ефрона
