ЭНТРОПИЯ

(от греч. entropia — поворот, превращение), понятие, впервые введённое в термодинамике для определения меры необратимого рассеяния энергии. Э. широко применяется и в др. областях науки: в статистической физике как мера вероятности осуществления к.-л. макроскопич. состояния; в теории информации как мера неопределённости к.-л. опыта (испытания), к-рый может иметь разные исходы. Эти трактовки Э. имеют глубокую внутр. связь. Напр., на основе представлений об информац. Э. можно вывести все важнейшие положения статистич. физики.

В термодинамике понятие «Э.» было введено нем. физиком Р. Клаузиусом (1865), к-рый показал, что процесс превращения теплоты в работу подчиняется определ. физ. закономерности — второму началу термодинамики, к-рое можно сформулировать строго математически, если ввести особую ф-цию состояния —Э. Так, для термодинамич. системы, совершающей квазистатически (бесконечно медленно) циклич. процесс, в к-ром система последовательно получает малые кол-ва теплоты dQ при соответствующих значениях абс. темп-ры Т, интеграл от «приведённого» кол-ва теплоты dQ/T по всему циклу равен нулю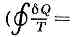

=0 — т. н. равенство Клаузиуса). Это равенство, эквивалентное второму началу термодинамики для равновесных процессов, Клаузиус получил, рассматривая произвольный циклич. процесс как сумму очень большого (в пределе бесконечно большого) числа элементарных Карно циклов. Математически равенство Клаузиуса необходимо и достаточно для того, чтобы выражение

dS=dQ/T (1)

представляло собой полный дифференциал ф-ции состояния S, назв. «Э.» (дифф. определение Э.). Разность Э. системы в двух произвольных состояниях А и В (заданных, напр., значениями темп-р и объёмов) равна:

SB-SA=?BAdQ/T (2)

(интегр. определение Э.). Интегрирование здесь ведётся вдоль пути любого квазистатич. процесса, связывающего состояния А и В, при этом, согласно равенству Клаузиуса, приращение Э. DS=SB-SA не зависит от пути интегрирования. Т. о., из второго начала термодинамики следует, что существует однозначная ф-ция состояния S, к-рая при квазистатич. адиабатич. процессах (dQ=0) остаётся постоянной. Процессы, в к-рых Э. остаётся постоянной, наз. изоэнтропийными. Примером может служить процесс, широко используемый для получения низких темп-р,— адиабатич. размагничивание (см. МАГНИТНОЕ ОХЛАЖДЕНИЕ). При изотермич. процессах изменение Э. равно отношению сообщённой системе теплоты к абс. темпре. Напр., изменение Э. при испарении жидкости равно отношению теплоты испарения к темп-ре испарения при условии равновесия жидкости с её насыщ. паром.

Согласно первому началу термодинамики, dQ=dU+pdV, т. е. сообщаемое системе кол-во теплоты равно сумме приращения внутренней энергии dU и совершаемой системой элем. работы pdV, где р — давление, V -объём системы. С учётом первого начала термодинамики дифф. определение Э. принимает вид:

dS =1/T(dU+pdV), (3)

откуда следует, что Э. представляет собой потенциал термодинамический при выборе в кач-ве независимых переменных внутр. энергии U и объёма V. Частные производные Э. связаны с Т и р соотношениями:

1/T=(дS/дU (4) и p/T-=(дS/дV)U (5) к-рые определяют уравнения состояния системы (первое — калорическое, второе — термическое). Ур-ние (4) лежит в основе определения абсолютной температуры (см. ТЕМПЕРАТУРА, ТЕМПЕРАТУРНЫЕ ШКАЛЫ).

Ф-ла (2) определяет Э. лишь с точностью до аддитивной постоянной (т. е. оставляет начало отсчёта Э. произвольным). Абс. значение Э. можно установить с помощью третьего начала термодинамики, основываясь на к-ром, за нач. точку отсчёта Э. принимают S0=0 при Т=0.

Важность понятия Э. для анализа необратимых (неравновесных) процессов также была показана впервые Клаузиусом. Для необратимых процессов интеграл от приведённой теплоты dQ/T по замкнутому пути всегда отрицателен.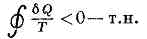

Клаузиуса неравенство. Это неравенство — следствие теоремы Карно: кпд частично или полностью необратимого циклич. процесса всегда меньше, чем кпд обратимого цикла. Из неравенства Клаузиуса вытекает, что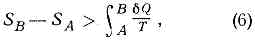

поэтому Э. адиабатически изолированной системы при необратимых процессах может только возрастать.

Т. о., О. определяет хар-р процессов в адиабатич. условиях: возможны только такие процессы, при к-рых Э. либо остаётся неизменной (обратимые процессы), либо возрастает (необратимые процессы). При этом не обязательно, чтобы возрастала Э. каждого из тел, участвующих в процессе. Увеличивается общая сумма Э. тел, в к-рых процесс вызвал изменения.

Термодинамич. равновесию адиабатич. системы соответствует состояние с максимумом Э. Энтропия может иметь не один, а неск. максимумов, при этом система будет иметь неск. состояний равновесия. Равновесие, к-рому соответствует наибольший максимум Э., наз. абсолютно устойчивым (стабильным). Из условия максимальности Э. адиабатич. системы в состоянии равновесия вытекает важное следствие: темп-ра всех частей системы в состоянии равновесия одинакова.

Понятие Э. применимо и к термодинамически неравновесным состояниям, если отклонения от термодинамики равновесия невелики и можно ввести представление о локальном термодинамическом равновесии в малых, но ещё макроскопич. объёмах. В целом Э. неравновесной системы равна сумме Э. её частей, находящихся в локальном равновесии.

Термодинамика неравновесных процессов позволяет более детально исследовать процесс возрастания Э. и вычислить кол-во Э., образующейся в ед. объёма в ед. времени вследствие отклонения от термодинамич. равновесия,— производство энтропии.

Статистич. физика связывает Э. с вероятностью осуществления данного макроскопич. состояния системы. Э. определяется через логарифм статистического веса W данного равновесного состояния:

S=klnW(?, N), (7)

где W(?, N)—число квантовомеханич. уровней в узком интервале энергии D? вблизи значения энергии ? системы из N ч-ц, в классич. статистич. физике W — величина объёма в фазовом пространстве системы при заданных ? и N. Впервые связь Э. с вероятностью состояния системы была установлена австр. физиком Л. Больцманом в 1872: возрастание Э. системы обусловлено её переходом из менее вероятного состояния в более вероятное. Иными словами, эволюция замкнутой системы осуществляется в направлении наиболее вероятного распределения энергии по отд. подсистемам.

В отличие от термодинамики, статистич. физика рассматривает особый класс процессов — флуктуации, при к-рых система переходит из более вероятного состояния в менее вероятное, и её Э. уменьшается. Наличие флуктуации показывает, что закон возрастания Э. выполняется только в ср. для большого промежутка времени.

Э. в статистич. физике тесно связана с информац. Э., к-рая служит мерой неопределённости сообщений (сообщения описываются множеством величин x1, х2, . . ., хn и вероятностей Р1, Р2,. . .,Рn появления этих величин в сообщении). Для определённого (дискретного) статистич. распределения вероятностей Рk информац. Э. называют величину

Hи=-Snk=1РkInPk при Snk=1Pk=1.(8)

Ни=0, если к.-л. из Рk равно 1, а ост.— нулю, т. е. информация достоверна, неопределённость отсутствует. Э. принимает наибольшее значение, когда все Pk одинаковы (неопределённость в информации максимальна). Информац. Э., как и термодинамическая, обладает св-вом аддитивности (Э. неск. сообщений равна сумме Э. отд. сообщений). Из вероятностной трактовки информац. Э. могут быть выведены осн. распределения статистич. физики: каноническое Гиббса распределение, к-рое соответствует макс. значению информац. Э. при заданной ср. энергии, и большое канонич. распределение Гиббса — при заданных ср. энергии и числе ч-ц в системе.