Характеристика
I
Характери́стика
в математике, 1) целая часть десятичного Логарифма.
2) Понятие теории дифференциальных уравнений (См. Дифференциальные уравнения) с частными производными.
Х. дифференциального уравнения 1-го порядка
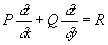 , (1)
, (1)
где Р = P (x, y, z), Q = Q (x, y, z), R = R (x, y, z) — заданные функции, называются кривые, определяемые системой обыкновенных дифференциальных уравнений
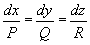 . (2)
. (2)
Интегрируя систему (2), получают семейство характеристик φ(x, y, z) = C1, ψ(x, y, z) = C2 (C1, C2 — произвольные постоянные) как совокупность кривых, касающихся в каждой своей точке вектора {P, Q, R}. Всякая интегральная поверхность уравнения (1) представляет собой геометрическое место Х., пересекающих некоторую кривую; уравнение такой поверхности может быть записано в виде F[φ(x, y, z), ψ(x, y, z)] = 0, где F — некоторая функция двух переменных. Обратно, чтобы найти интегральную поверхность, проходящую через заданную кривую (см. Коши задача), достаточно построить геометрическое место Х., пересекающих эту кривую. Задача Коши имеет одно и только одно решение, если заданная кривая не является Х. Понятие Х. обобщается на случай дифференциального уравнения 1-го порядка с числом независимых переменных, большим двух.
Х. дифференциального уравнения 2-го порядка
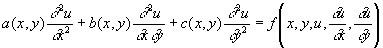 (3)
(3)
были введены Г. Монжем (1784, 1795) как линии, вдоль которых удовлетворяется обыкновенное дифференциальное уравнение
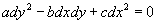 . (4)
. (4)
Если уравнение (3) принадлежит к гиперболическому типу, то получаются два семейства Х. с уравнениями ξ(x, y) = C1 и η(х, у) = C2 (C1, C2 — произвольные постоянные); взяв ξ и η за новые аргументы, можно привести уравнение (3) к виду
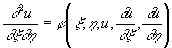 .
.
Для уравнения (3) параболического типа эти семейства совпадают; если выбрать аргумент η произвольно, то уравнение (3) приведется к виду
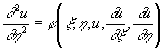 .
.
Уравнение (3) эллиптического типа не имеет вещественных Х.; если записать решение уравнения (4) в виде ξ ± iη = C, то уравнение (3) преобразуется к виду
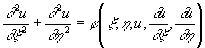 .
.
Значения решения и вдоль Х. и значения 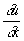 и
и 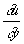 в какой-либо её точке полностью определяют значения этих производных вдоль всей линии [на этом основан т. н. метод Х. решения краевых задач (См. Краевые задачи) для уравнения (3)]; для других линий такой связи нет. С другой стороны, значения u,
в какой-либо её точке полностью определяют значения этих производных вдоль всей линии [на этом основан т. н. метод Х. решения краевых задач (См. Краевые задачи) для уравнения (3)]; для других линий такой связи нет. С другой стороны, значения u, 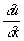 и
и 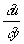 , заданные на линии, не являющейся Х., определяют значения решения вблизи этой линии; для Х. же это не так. Если два решения уравнения (3) совпадают по одну сторону от некоторой линии и различны по другую, то эта линия непременно является Х.
, заданные на линии, не являющейся Х., определяют значения решения вблизи этой линии; для Х. же это не так. Если два решения уравнения (3) совпадают по одну сторону от некоторой линии и различны по другую, то эта линия непременно является Х.
Если коэффициенты уравнения (3) зависят от u, 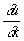 и
и 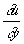 (квазилинейный случай), то Х., определяемые из уравнения (4), будут разные для разных решений. Имеются определения Х. и для уравнений и систем уравнений с частными производными любого порядка.
(квазилинейный случай), то Х., определяемые из уравнения (4), будут разные для разных решений. Имеются определения Х. и для уравнений и систем уравнений с частными производными любого порядка.
Лит. см. при ст. Уравнения математической физики.
II
Характери́стика
в технике, взаимосвязь между зависимыми и независимыми переменными, определяющими состояние технического объекта (процесса, прибора, устройства, машины, системы), выраженная в виде текста, таблицы, математической формулы, графика и т.п. Например, зависимости тока от электрического напряжения на участке электрической цепи (см. Вольтамперная характеристика), расхода топлива автомобилем от пройденного им пути и состояния дороги, громкости и качества звучания громкоговорителя от частоты, времени перемагничивания ферритового сердечника от величины намагничивающего поля.
Х. по методике определения подразделяют на детерминированные (статические, динамические) и статистические; по виду аналитические зависимости — на линейные и нелинейные; по назначению — на эксплуатационные, настроечные и т.д. Статической Х. называется зависимость между выходной и входной величинами технической системы в установившихся состояниях. Динамические Х. (частотные, импульсные и др.) отражают реакции изучаемой системы на какие-либо типовые возмущающие воздействия: например, частотная Х. отражает зависимость амплитуды и фазы периодического сигнала на выходе системы от амплитуды и фазы входного гармонического сигнала при изменении только его частоты; импульсная Х. — зависимость изменения во времени сигнала на выходе системы от воздействия входного единичного импульса. В наиболее полной форме динамическая Х. содержатся в динамической математической модели объекта, например в виде дифференциальных уравнений. Статистические Х. (оценки) применяют к объектам, поведение которых во времени меняется случайным образом. К статистическим Х. относятся, например, дисперсия, автокорреляционная функция, спектральная плотность и т.п.
Линейными называются все Х., которые могут быть с заданной точностью аппроксимированы выражением вида у = ax + b, где у — выходное воздействие, x — входное воздействие изучаемой системы, а и b — постоянные коэффициенты. Все остальные Х. — нелинейные; среди них выделяют линеаризуемые Х., которые по частям с известной точностью аппроксимируются указанным выше выражением (см. Линеаризация).
А. В. Кочеров.
Значения в других словарях
- характеристика — -и, ж. 1. Описание характерных, отличительных свойств, черт кого-, чего-л. Перед нами лежит несколько сочинений, имеющих предметом характеристику провинции и ее существеннейших интересов. Салтыков-Щедрин, Письма о провинции. Малый академический словарь
- Характеристика — Одно из основных понятий в теории дифференциальных уравнений с частными производными. Роль X. проявляется в существенных свойствах этих уравнений, таких, как локальные свойства решений, разрешимость различных задач, их корректность и др. Математическая энциклопедия
- ХАРАКТЕРИСТИКА — ХАРАКТЕРИСТИКА — англ. char — acteristic; нем. Charakteristik. attestation; 1. Совокупность признаков, свойств, черт человека, предмета, явления и т. п. 2. Официальный документ о служебной, общественной и т. д. деятельности к.-л. 3. Целая часть десятичного логарифма. Социологический словарь
- характеристика — орф. характеристика, -и Орфографический словарь Лопатина
- характеристика — Характер/и́ст/ик/а. Морфемно-орфографический словарь
- характеристика — (официальный документ, содержащий отзыв о чьей-л. служебной и общественной деятельности) к о г о и (во избежание двузначности) н а к о г о . Характеристика аспиранта. Характеристика претендента на занятие должности. Управление в русском языке
- характеристика — ХАРАКТЕРИСТИКА и, ж. caractéristique f., пол. charakteristyka, нем. Charakteristik. 1. Описание, обрисовка, определение существенных особенностей, признаков кого-, чего-н. БАС-1. Словарь галлицизмов русского языка
- характеристика — • всесторонняя ~ • исчерпывающая ~ • яркая ~ Словарь русской идиоматики
- Характеристика — ХАРАКТЕРИСТИКА (Χαράσσω — черчу). Выбор из многообразия признаков, которые несет от каждого предмета или явления окружающей нас действительности наше восприятие, самого существенного, определяющего... Словарь литературных терминов
- характеристика — сущ., ж., употр. сравн. часто (нет) чего? характеристики, чему? характеристике, (вижу) что? характеристику, чем? характеристикой, о чём? о характеристике; мн. что? характеристики, (нет) чего? характеристик, чему? характеристикам, (вижу) что?... Толковый словарь Дмитриева
- характеристика — ХАРАКТЕРИСТИКА, и, ж. 1. Описание характерных, отличительных качеств, черт кого-чего-н. Блестящая х. исследования. Х. эпохи. 2. Официальный документ с отзывом о служебной, общественной деятельности кого-н. Х. с места работы. Толковый словарь Ожегова
- характеристика — ХАРАКТЕР’ИСТИКА, характеристики, ·жен. (от ·греч. charakter). 1. Описание, определение отличительных свойств, достоинств и недостатков кого-чего-нибудь. «Общая характеристика коммунистического общества дана в трудах Маркса, Энгельса и Ленина.» Сталин. Толковый словарь Ушакова
- характеристика — ХАРАКТЕРИСТИКА -и; ж. 1. Описание характерных, отличительных свойств, черт кого-, чего-л. Негативная х. деятельности. Что придумаете для характеристики каждого из нас? Статья содержит положительную характеристику основных законов. Толковый словарь Кузнецова
- характеристика — См. характер Толковый словарь Даля
- Характеристика — См. Логарифм. Энциклопедический словарь Брокгауза и Ефрона
- характеристика — Характеристики, ж. [от греч. charakter]. 1. Описание, определение отличительных свойств, достоинств и недостатков кого-чего-н. 2. Официальный документ с отзывом о служебной, общественной деятельности кого-л. 3. Целая часть десятичного логарифма (мат.). Большой словарь иностранных слов
- ХАРАКТЕРИСТИКА — ХАРАКТЕРИСТИКА — целая часть десятичного логарифма. Напр., lg 300 = 2,4771, где 2 есть характеристика для lg 300; lg 0,3 = ,4771, где = -1 есть характеристика для lg 0,3. ХАРАКТЕРИСТИКА — .. Большой энциклопедический словарь
- ХАРАКТЕРИСТИКА — 1) описание, определение отличительных свойств, качеств кого-либо или чего-либо; 2) официальный документ с отзывом о деятельности конкретного человека. Экономический словарь терминов
- характеристика — характеристика ж. 1. Описание характерных, отличительных свойств, достоинств и недостатков кого-либо или чего-либо. || Результат такого описания. 2. Заключение о чьей-либо трудовой и общественной деятельности как официальный документ. Толковый словарь Ефремовой
