Ряд

I

бесконечная сумма, например вида

u₁ + u₂ + u₃ +... + u_n +...

или, короче,

. (1)

Одним из простейших примеров Р., встречающихся уже в элементарной математике, является сумма бесконечно убывающей геометрической прогрессии

1 + q + q ² +... + q ⁿ +... = 1/(1 — q), ∣q∣< 1. (2)

Р. широко используются в математике и её приложениях как в теоретических исследованиях, так и при приближённых численных решениях задач. Многие числа могут быть записаны в виде специальных Р., с помощью которых удобно вычислять их приближённые значения с нужной точностью. Например, для числа π имеется Р.

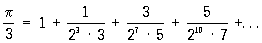, (3)

для основания е натуральных логарифмов — Р.

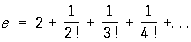, (4)

а для натурального логарифма In2 — ряд

.

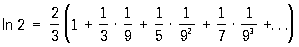Метод разложения в Р. является эффективным методом изучения функций. Он применяется для вычисления приближённых значений функций, для вычисления и оценок интегралов, для решения всевозможных уравнений (алгебраических, дифференциальных, интегральных) и т. п.

При численных расчётах, когда Р. заменяется конечной суммой его первых слагаемых, полезно иметь оценку получаемой при этом погрешности (оценку «скорости сходимости» Р.). При этом целесообразно использовать Р., у которых эти погрешности достаточно быстро стремятся к нулю с возрастанием номера n. Например, в случае Р. (4) оценка указанной погрешности имеет вид 0 < е — s_n < 1/n! n.

Одни и те же величины могут выражаться через суммы различных рядов. Так, для числа π, кроме Р. (3), имеются и другие Р., например

,

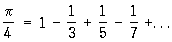однако он сходится значительно «медленнее» Р. (3), и потому его невыгодно использовать для приближённого вычисления числа π. Существуют методы преобразования Р., иногда улучшающие скорость сходимости Р.

На бесконечные суммы не переносятся все свойства конечных сумм. Например, если взять Р.

1 — 1 + 1 — 1 +... (5)

и сгруппировать подряд его члены по два, то получим (1—1) + (1—1) +... = 0; при другом же способе группировки 1 — (1 — 1) — (1 — 1) —... = 1. Поэтому следует дать чёткое определение того, что называется бесконечной суммой, и, определив это понятие, проверить, справедливы ли для таких сумм закономерности, установленные для конечных сумм. Доказывается, что для бесконечного числа слагаемых при определённых условиях сохраняются законы коммутативности и ассоциативности сложения, дистрибутивности умножения относительно сложения, правила почленного дифференцирования и интегрирования и т. п.

Числовые ряды. Формально Р. (1) можно определить как пару числовых (действительных или комплексных) последовательностей {u_n} и {S_n} таких, что S_n = u₁ +... + u_n, n = 1, 2,... Первая последовательность называется последовательностью членов Р., а вторая — последовательностью его частичных сумм [точнее S_n называется частичной суммой n-го порядка Р. (1)]. Р. (1) называется сходящимся, если сходится последовательность его частичных сумм {S_n}. В этом случае предел

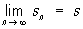
называется суммой Р. и пишется

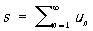
Т. о., обозначение (1) применяется как для самого Р., так и для его суммы (если он сходится). Если последовательность частичных сумм не имеет предела, то Р. называется расходящимся. Примером сходящегося Р. является Р. (2), расходящегося — Р. (5). Каждый Р. однозначно определяет последовательность его частичных сумм, и обратно: для любой последовательности {s_n} имеется и притом единственный Р., для которого она является последовательностью его частичных сумм, причём члены u_n этого Р. определяются по формулам u₁ = s₁,..., u_n+1 = s_n+1 — s_n,..., n = 1, 2,... В силу этого изучение Р. эквивалентно изучению последовательностей.

Р. 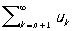называется остатком порядка n Р. (1). Если Р. сходится, то каждый его остаток сходится, а если какой-либо остаток Р. сходится, то и сам Р. также сходится. Если остаток порядка n Р. (1) сходится и его сумма равна r_n, то s = s_n + r_п.

Если Р. (1) и Р.

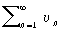
сходятся, то сходится и Р.

,

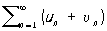называемый суммой рядов (1) и (6), причем его сумма равна сумме данных Р. Если Р.(1) сходится и λ — комплексное число, то Р.

,

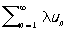называемый произведением Р. на число λ, также сходится и

.

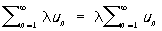Условие сходимости Р., не использующее понятия его суммы (в случаях, когда, например, сумма Р. неизвестна), даёт критерий Коши: для того чтобы Р. (1) сходился, необходимо и достаточно, чтобы для любого ε > 0 существовал такой номер n_ε, что при любом n ≥ n_ε и любом целом р ≥ 0 выполнялось неравенство

.

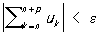Отсюда следует, что если Р. (1) сходится, то

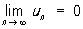
Обратное неверно: n-й член так называемого гармонического ряда (См. Гармонический ряд)

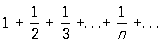
стремится к нулю, однако этот Р. расходится.

Большую роль в теории Р. играют Р. с неотрицательными членами. Для того чтобы такой Р. сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху. Если же он расходится, то

,

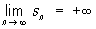поэтому в этом случае пишут

.

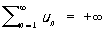Для Р. с неотрицательными членами имеется ряд признаков сходимости.

Интегральный признак сходимости: если функция f (х) определена при всех х ≥ 1, неотрицательна и убывает, то Р.

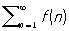(7)

сходится тогда и только тогда, когда сходится интеграл

.

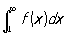С помощью этого признака легко устанавливается, что Р.

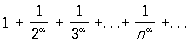(8)

сходится при α > 1 и расходится при α ≤ 1.

Признак сравнения: если для двух Р. (1) и (6) с неотрицательными членами существует такая постоянная с > 0, что 0 ≤ u_n ≤ c υ_n, то из сходимости Р. (6) следует сходимость Р. (1), а из расходимости Р. (1) — расходимость Р. (6). Обычно для сравнения берётся Р. (8), а в заданном Р. выделяется главная часть вида А/n ^α. Таким методом сразу получается, что Р. с n-м членом

,

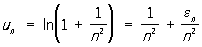где

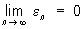
сходится, поскольку сходится Р.

.

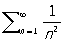Как следствие признака сравнения получается следующее правило: если

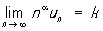
то при α > 1 и 0 ≤ k < + ∞ Р. сходится, а при α ≤ 1 и 0 < k ≤ + ∞ Р. расходится. Так, например, Р. с n-м членом u_n = sin (1/n ²) сходится, ибо

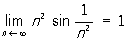(α = 2)

a Р. с u_n = tg (π/n) расходится, здесь

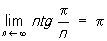(α = 1)

Часто оказываются полезными два следствия признака сравнения. Признак Д'Аламбера: если существует 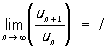(u_n > 0), то при l < 1 P. (1) сходится, а при l > 1 — расходится; и признак Коши: если существует 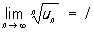(u_n ≥ 0), то при l < 1 P. (1) сходится, а при l > 1 P. расходится. При I = 1 как в случае признака Д'Аламбера, так и в случае признака Коши существуют и сходящиеся и расходящиеся Р.

Важный класс Р. составляют абсолютно сходящиеся ряды: Р. (1) называется абсолютно сходящимся, если сходится Р.

.

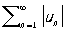Если Р. абсолютно сходится, то он и просто сходится. Р.

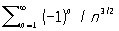
абсолютно сходится, а Р.

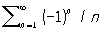
сходится, но не абсолютно. Сумма абсолютно сходящихся Р. и произведение абсолютно сходящегося Р. на число являются также абсолютно сходящимися Р. На абсолютно сходящиеся Р. наиболее полно переносятся свойства конечных сумм. Пусть

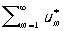(9)

— P., составленный из тех же членов, что и Р. (1), но взятых, вообще говоря, в другом порядке. Если Р. (1) сходится абсолютно, то Р. (9) также сходится и имеет ту же сумму, что и Р. (1). Если Р. (1) и Р. (6) абсолютно сходятся, то Р., полученный из всевозможных попарных произведений u_mυ_n членов этих Р., расположенных в произвольном порядке, также абсолютно сходится, причём если сумма этого Р. равна s, а суммы Р. (1) и (6) равны соответственно s₁ и s₂, то s = s₁s₂, т. е. абсолютно сходящиеся Р. можно почленно перемножать, не заботясь о порядке членов. Признаки сходимости для Р. с неотрицательными членами применимы для установления абсолютной сходимости рядов.

Для Р., не абсолютно сходящихся (такие Р. называют также условно сходящимися), утверждение о независимости их суммы от порядка слагаемых неверно. Справедлива теорема Римана: посредством надлежащего изменения порядка членов данного не абсолютно сходящегося Р. можно получить Р., имеющий наперёд заданную сумму, или расходящийся Р. Примером условно сходящегося Р. может служить Р.

.

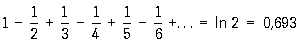Если в этом Р. переставить члены так, чтобы за двумя положительными следовал один отрицательный:

,

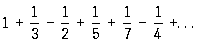то его сумма увеличится в 1,5 раза. Существуют признаки сходимости, применимые к не абсолютно сходящимся Р. Например, признак Лейбница: если

, ,

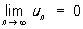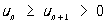то знакочередующийся Р.

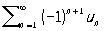(10)

сходится. Более общие признаки можно получить, например, с помощью преобразования Абеля для Р., представимых в виде

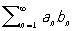. (11)

Признак Абеля: если последовательность {a_n} монотонна и ограничена, а Р.

∑^∞_n=1b_n

сходится, то Р. (11) также сходится. Признак Дирихле: если последовательность {a_n} монотонно стремится к нулю, а последовательность частичных сумм Р.

∑^∞_n=1b_n

ограничена, то Р. (11) сходится. Например, по признаку Дирихле Р.

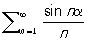
сходится при всех действительных α.

Иногда рассматриваются Р. вида

.

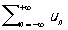Такой Р. называется сходящимся, если сходятся Р.

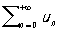и

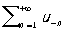
сумма этих Р. называется суммой исходного Р.

Р. более сложной структуры являются кратные ряды, т. е. Р. вида

,

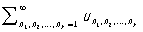где 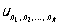— заданные числа (вообще говоря, комплексные), занумерованные k индексами, n₁, n₂,..., n_k, каждый из которых независимо от других пробегает натуральный ряд чисел. Простейшие из Р. этого типа — двойные ряды (См. Двойной ряд).

Для некоторых числовых Р. удаётся получить простые формулы для величины или оценки их остатка, что весьма важно, например, при оценке точности вычислений, проводимых с помощью Р. Например, для суммы геометрической прогрессии (2)

r_n = qⁿ⁺¹/(1 — q), ∣q∣< 1,

для P. (7) при сделанных предположениях

,

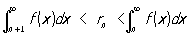а для P. (10)

∣r_n∣ ≤ u_n+1

С помощью некоторых специальных преобразований иногда удаётся «улучшить» сходимость сходящегося Р. В математике используются не только сходящиеся Р., но и расходящиеся. Для последних вводятся более общие понятия суммы Р. (см. Суммирование рядов и интегралов). Так, например, расходящийся Р. (5) можно просуммировать определённым способом к ¹/₂.

Функциональные ряды. Понятие Р. естественным образом обобщается на случай, когда членами Р. являются функции u_n = u_n (x) (действительные, комплексные или, более общо, функции, значения которых принадлежат какому-то метрическому пространству), определённые на некотором множестве Е. В этом случае ряд

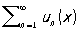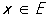, (11)

называется функциональным.

Если Р. (11) сходится в каждой точке множества Е, то он называется сходящимся на множестве Е. Пример: Р. 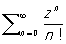сходится на всей комплексной плоскости. Сумма сходящегося Р. непрерывных, например, на некотором отрезке, функций не обязательно является непрерывной функцией. Условия, при которых на функциональные Р. переносятся свойства непрерывности, дифференцируемости и интегрируемости конечных сумм функций, формулируются в терминах равномерной сходимости Р. Сходящийся Р. (11) называется равномерно сходящимся на множестве Е, если во всех точках Е отклонение частичных сумм Р.

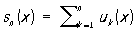
при достаточно больших номерах n от суммы Р.

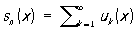
не превышает одной и той же сколь угодно малой величины, точнее, каково бы ни было наперёд заданное число ε > О, существует такой номер n_ε, что

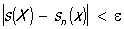
для всех номеров n ≤ n_ε и всех точек х ∈ Е. Это условие равносильно тому, что

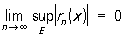
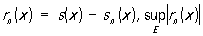[ — верхняя грань 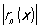на Е]. Например, Р.

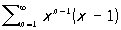
равномерно сходится на отрезке [0, q] при 0 < q < 1 и не сходится равномерно на отрезке [0, 1].

Критерий Коши: для того чтобы Р. (11) равномерно сходился на множестве Е, необходимо и достаточно, чтобы для любого ε > 0 существовал такой номер n_ε, что для всех номеров п ≥ n_ε, р … 0 и всех точек 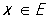выполнялось неравенство

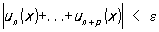
Признак Вейерштрасса: если существует такой сходящийся числовой Р.

,

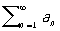что 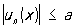|, , 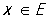n = 1, 2,..., то Р. (11) равномерно сходится на Е.

Сумма равномерно сходящегося Р. непрерывных на некотором отрезке (или, более общо, на некотором топологическом пространстве) функций является непрерывной на этом отрезке (пространстве) функцией. Сумма равномерно сходящегося Р. интегрируемых на некотором множестве функций является интегрируемой на этом множестве функцией, и Р. можно почленно интегрировать. Если последовательность частичных сумм Р. интегрируемых функций сходится в среднем к некоторой интегрируемой функции, то интеграл от этой почти всюду сходящейся последовательностью частичных сумм является равномерной функции равен сумме Р. из интегралов от членов Р. Интегрируемость в этих теоремах понимается в смысле Римана или Лебега. Для интегрируемых по Лебегу функций достаточным условием возможности почленного интегрирования Р. с почти всюду сходящейся последовательностью частичных сумм является равномерная оценка их абсолютных величин некоторой интегрируемой по Лебегу функцией. Если члены сходящегося на некотором отрезке Р. (11) дифференцируемы на нём и Р. из их производных сходится равномерно, то сумма Р. также дифференцируема на этом отрезке и Р. можно почленно дифференцировать.

Понятие функционального Р. обобщается и на случай кратных Р. В различных разделах математики и её приложениях широко используется разложение функции в функциональные Р., прежде всего в степенные ряды (См. Степенной ряд), тригонометрические ряды (См. Тригонометрический ряд) и, более общо, в Р. по специальным функциям некоторых операторов.

К понятию бесконечных сумм подошли ещё учёные Древней Греции, у них уже встречалась сумма членов бесконечной геометрической прогрессии с положительным знаменателем меньшим единицы. Как самостоятельное понятие Р. вошёл в математику в 17 в. И. Ньютон и Г. Лейбниц систематически использовали Р. для решения уравнений как алгебраических, так и дифференциальных. Формальная теория Р. успешно развивалась в 18—19 вв. в работах Я. и И. Бернулли, Б. Тейлора, К. Маклорена, Л. Эйлера, Ж. Д' Аламбера (См. Д'Аламбер), Ж. Лагранжа и др. В этот период использовались как сходящиеся, так и расходящиеся Р., хотя не было полной ясности в вопросе о законности действий над ними. Точная теория Р. была создана в 19 в. на основе понятия Предела в трудах К. Гаусса, Б. Больцано, О. Коши, П. Дирихле, Н. Абеля (См. Абель), К. Вейерштрасса, Г. Римана и др.

Лит.: Маркушевич А. И., Ряды. Элементарный очерк, 3 изд., М., 1957; Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1—2, М., 1971—73; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1—2, М., 1973; Никольский С. М., Курс математического анализа, т. 1—2, М., 1973; Бахвалов Н. С., Численные методы, М., 1973.

Л. Д. Кудрявцев.

II

таксономическая категория, применяемая в ботанике; то же, что Серия.