Матрица
I
Ма́трица (нем. Matrize, от латинского matrix — матка, источник, начало)
в полиграфии,
1) сменный элемент литейной формы с углублённым (иногда фотографическим) изображением буквы или знака, используемый при отливке типографских литер или шрифтовых строк. М. — металлический брусок, на одной из граней которого выштамповано (путём вдавливания пуансона) или выгравировано очко буквы или знака. При заполнении жидким сплавом полости литейной формы и очка на М., прижатой к форме, образуются типографские литеры или шрифтовые строки с рельефной печатной поверхностью. В зависимости от типа машины, на которой производится отливка литер или строк, различают шрифтолитейные, строкоотливные и буквоотливные М.
Шрифтолитейная М. — стальной брусок прямоугольного сечения с углублённым изображением одной буквы или знака. Комплект шрифтолитейных М. позволяет отливать на шрифтолитейной машине все литеры одного шрифта, используемые для ручного набора.
В строкоотливной наборной машине (см. Линотип) из отдельных М., хранящихся в магазине, составляется матричная строка, устанавливаемая перед щелью литейной формы. После заполнения формы сплавом образуется цельнометаллическая шрифтовая строка.
В буквоотливной наборной машине (см. Монотип) комплект М. собран в матричной рамке. При отливке необходимая М. устанавливается над щелью отливной формы. В отличие от строкоотливной шрифтовая строка на буквоотливной наборной машине образуется из отдельных литер. Монотипная М. снабжена отверстием для нанизывания на стержень матричной рамки и коническим углублением для точной установки и прижима М. к литейной форме.
В фотонаборных машинах (См. Фотонаборная машина) используются М., в которых углублённые изображения знаков заменены фотографическими.
2) Углублённый оттиск с рельефной печатной формы на пластичном материале (картоне, пластмассе и т. д.), используемый для получения стереотипных копий печатной формы (см. Матрицирование, Стереотипия).
Г. С. Ершов.
II
Ма́трица
в математике, система элементов aij (чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной схемы. Если схема имеет m строк и n столбцов, то говорят о (m × n)-матрице. Обозначения:
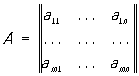
или 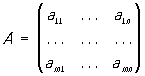 .
.
Короче: 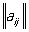 ,
, 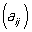 . Наряду с конечными М. рассматриваются М. с бесконечным числом строк или столбцов.
. Наряду с конечными М. рассматриваются М. с бесконечным числом строк или столбцов.
М., состоящая из одной строки, называется строкой, из одного столбца — столбцом. Если m = n, то М. называется квадратной, а число n — её порядком. Квадратная М., у которой отличны от нуля лишь диагональные элементы αi = αii называется диагональной и обозначается diag(α1, ..., αn). Если все αi = α, получают скалярную М. При α = 1 М. называется единичной и обозначается Е. М., все элементы которой равны нулю, называется нулевой.
Переставив в М. строки со столбцами, получают транспонированную М. A’, или AT. Если элементы М. заменяют на комплексно-сопряжённые, получают комплексно-сопряжённую М. А. Если элементы транспонированной М. A’ заменяют на комплексно-сопряжённые, то получают М. А*, называется сопряжённой с А. Определитель квадратной М. А обозначается ∣A∣ или det A. Минором k-го порядка М. А называется определитель k-го порядка, составленный из элементов, находящихся на пересечении некоторых k строк и k столбцов М. A в их естественном расположении. Рангом М. А называется максимальный порядок отличных от нуля миноров матрицы.
Действия над матрицами. Произведением прямоугольной (m × n)-матрицы А на число ее называют М., элементы которой получены из элементов aij умножением на число α:
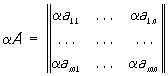
Сумма определяется для прямоугольных М. одинакового строения, и элементы суммы равны суммам соответствующих слагаемых, то есть
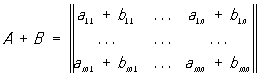
Умножение М. определяется только для прямоугольных М. таких, что число столбцов первого множителя равно числу строк второго. Произведением (m × р)-матрицы А на (р × n)-матрицу В будет (m × n)-матрица С с элементами
cij = ai1b1j + ai2b2j + ... + aipbpj,
i = 1, ..., m, j = 1, ..., n.
Введённые три действия над М. обладают свойствами, близкими к свойствам действий над числами. Исключением является отсутствие коммутативного закона при умножении М.: равенство AB = BA может не выполняться. Матрицы А и В называются перестановочными, если AB = BA. Кроме того, произведение двух М. может равняться нулевой М., хотя каждый сомножитель отличен от нулевой. Справедливы правила:
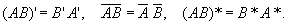
Определитель произведения двух квадратных М. равен произведению определителей перемножаемых М.
Часто удобно разбивать М. на клетки, являющиеся М. меньших размеров, проводя разделительные линии через всю М. слева направо или сверху вниз. При умножении такой так называемой клеточной М. на число, нужно умножить все её клетки на то же число. При надлежащем согласовании разбиений действия сложения и умножения клеточных М. осуществляются так, как будто вместо клеток стоят числа.
Квадратная М. А = (aij) называется неособенной, или невырожденной, если её определитель не равен нулю; в противном случае М. называется особенной (вырожденной). М. А-1 называется обратной к квадратной М. А, если AA-1 = E, при этом 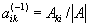 . Неособенность М. А есть необходимое и достаточное условие существования обратной М., которая при этом оказывается единственной и перестановочной с исходной М. Верна формула: (AB)-1 = B-1A-1.
. Неособенность М. А есть необходимое и достаточное условие существования обратной М., которая при этом оказывается единственной и перестановочной с исходной М. Верна формула: (AB)-1 = B-1A-1.
Большой интерес приобретает обобщённая обратная (или псевдообратная) М. А+, определяемая как для любой прямоугольной М., так и для особенной квадратной. Эта М. определяется из четырёх равенств:
AA+A = A, А+АА+ = А, AA+ = (AA+)*, А+А = (А+А)*.
Квадратные матрицы. Степенью An М. А называется произведение n сомножителей, равных А. Выражение вида α0Аn + α1An-1 + ... + αnE, где α0, α1, ..., αn — числа, называется значением полинома α0tn + αitn-1 + ... + αnE от квадратной М. А. Правила действий над полиномами от данной М. А ничем не отличаются от правил действий над алгебраическими многочленами. Можно рассматривать и аналитические функции от М. В частности, если
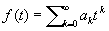
есть сходящийся на всей комплексной плоскости ряд (например, 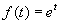 ), то и бесконечный ряд
), то и бесконечный ряд 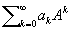 оказывается сходящимся при любой М. А, его сумму естественно считать равной f(A). Если же ряд f(t) сходится в некотором конечном круге сходимости, то f(A) задаётся этим рядом для достаточно «малых» М.
оказывается сходящимся при любой М. А, его сумму естественно считать равной f(A). Если же ряд f(t) сходится в некотором конечном круге сходимости, то f(A) задаётся этим рядом для достаточно «малых» М.
Аналитические функции от М. играют большую роль в теории дифференциальных уравнений. Так, система обыкновенных дифференциальных уравнений с постоянными коэффициентами, записанных в матричных обозначениях в виде
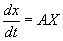
(здесь Х — столбец из неизвестных функций), имеет решение х = eAtC, где С — столбец из произвольных постоянных.
Ненулевой столбец Х такой, что AX = λХ, называется собственным вектором М. А. В этом равенстве коэффициент λ может быть лишь одним из корней многочлена
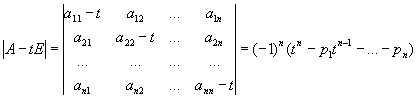
который называется характеристическим многочленом М. А. Эти корни называются собственными значениями, или характеристическими числами, М. А. Коэффициенты характеристического многочлена выражаются через суммы некоторых миноров М. А. В частности, p1 = a11 + ... + a1n = SpA (след A), 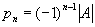 . Справедливо соотношение Кэли — Гамильтона: если φ(f) есть характеристический многочлен М. А, то φ(A) = 0, так что М. А является «корнем» своего характеристического многочлена.
. Справедливо соотношение Кэли — Гамильтона: если φ(f) есть характеристический многочлен М. А, то φ(A) = 0, так что М. А является «корнем» своего характеристического многочлена.
М. А называется подобной М. В, если существует такая неособенная М. С, что В = С-1AС. Легко проверяется, что подобные М. имеют одинаковые характеристические многочлены.
Исчисление матриц. М. — полезный аппарат для исследования многих задач теоретической и прикладной математики. Одной из важнейших задач является задача нахождения решения систем линейных алгебраических уравнений. В матричных обозначениях такие системы записываются в виде
AX = F,
где A есть М. коэффициентов, Х — искомое решение, записанное в виде столбца из n элементов, F — столбец свободных членов из m элементов. Если А — квадратная неособенная М., то система имеет единственное решение Х = A -1F. Если A прямоугольная (m × n-матрица ранга k, то решение может не существовать или быть не единственным. В случае несуществования решения имеет смысл обобщённое решение, дающее минимум сумме квадратов невязок (см. Наименьших квадратов метод). При отсутствии единственности точного или обобщённого решения часто выбирают нормальное решение, то есть решение с наименьшей суммой квадратов компонент. Нормальное обобщённое решение находится по формуле Х = A + F. Наиболее важен случай переопределённой системы: k = n < m. В этом случае обобщённое решение единственно. При k = m < n (недоопределённая система) точных решений бесконечно много и формула даёт нормальное решение.
Не менее важной для многочисленных приложений (в теории дифференциальных уравнений, в теории малых колебаний, в квантовой механике и т. д.) является задача решения полной или частичной проблемы собственных значений. Здесь ищутся все или часть собственных значений М. и принадлежащие им собственные или корневые (некоторые обобщения собственных) векторы. К этой задаче близко примыкает и обобщённая проблема собственных значений, в которой ищутся числа и векторы такие, что AX = λBX (А и В — заданные М.), и многие родственные проблемы.
С полной проблемой непосредственно связана также задача о приведении преобразованиями подобия квадратной М. к каноническjй форме. Такой формой будет diag (λ1, ..., λn), если М. имеет n различных собственных значений λ1, ..., λn, или форма Жордана [см. Нормальная (жорданова) форма матрицы (См. Нормальная форма матриц)] в общем случае.
Ввиду большой практической важности поставленных задач для их численного решения имеется большое число различных методов. Наряду с нахождением численного решения важно оценивать качество найденного решения и исследовать устойчивость решаемой задачи.
Матрицы специального типа. Существует большое число различных типов М. в зависимости от выполнения различных соотношений между элементами.
| Название матрицы | Определяющее условие | |
|---|---|---|
| Симметричная | 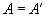 |
|
| Кососимметричная | 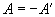 |
|
| Ортогональная | 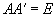 или или 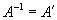 |
|
| Стохастическая | 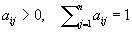 |
|
| Эрмитова | 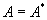 |
|
| Унитарная | 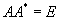 или или 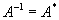 |
Некоторые типы естественно возникают в приложениях. Приведённая таблица даёт ряд важных типов квадратных М.
Следует отметить также ленточные М. — такие М., ненулевые элементы которых могут располагаться на главной диагонали и на диагоналях, соседних с главной, например, двухдиагональные и трёхдиагональные М. Не менее важны специальные типы М., употребляемых в качестве вспомогательных. Это элементарные М. — М., отличающиеся от единичной одним элементом; М. вращения и отражения.
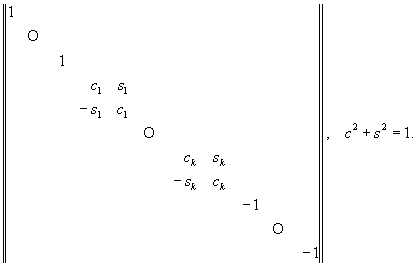
Имеются унитарные аналоги М. вращения и отражения; правые (левые) треугольные М. — М., у которых равны нулю элементы под (над) главной диагональю; правые (левые) почти треугольные М. (М. типа Хессенберга) — М., у которых равны нулю элементы под (над) диагональю, соседней снизу (сверху) с главной.
Преобразование матриц. Численные методы решения систем линейных уравнений основываются обычно на преобразовании систем посредством цепочки левых умножений на подходящие вспомогательные М. с тем, чтобы перейти к легко решаемой системе. В качестве вспомогательных для вещественных М. употребляются элементарные М., М. вращения или М. отражения. Система с неособенной М. приводится либо к системе с треугольной М., либо с ортогональной. В теоретическом аспекте это равносильно представлению М. коэффициентов в виде произведения двух треугольных М. (при выполнении некоторых дополнительных условий) или в виде произведения треугольной на ортогональную (в том или другом порядке).
Для переопределённой системы умножением слева на цепочку М. вращения или отражения можно прийти к системе с треугольной М. порядка n, решение которой даёт обобщённое решение исходной системы.
Для решения проблемы собственных значений, раньше чем применять наиболее эффективные итерационные методы, целесообразно подобно преобразовать М. общего вида к М. типа Хессенберга или к трёх диагональной в случае симметрии. Этого можно добиться за счёт цепочки подобных преобразований элементарными М., М. вращения или М. отражения.
Историческая справка. Понятие М. было введено в работах У. Гамильтона и А. Кэли в середине 19 века. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом (2-я половина 19 века и начало 20 века). И. А. Лаппо-Данилевский разработал теорию аналитических функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитическими коэффициентами. Матричные обозначения получили распространение в современной математике и её приложениях. Исчисление М. развивается в направлении построения эффективных алгоритмов для численного решения основных задач.
Лит.: Смирнов В. И., Курс высшей математики, 9 изд., т. 3, ч. 1, М., 1967; Мальцев А. И., Основы линейной алгебры, 3 изд., М., 1970; Гантмахер Ф. Р., Теория матриц, 3 изд., М., 1967; Уилкинсон Дж. Х., Алгебраическая проблема собственных значений, перевод с английского, М., 1970; Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы линейной алгебры, 2 изд., М. — Л., 1963; Воеводин В. В., Численные методы алгебры. Теория и алгорифмы, М., 1966; Лаппо-Данилевский И. А., Применение функций от матриц к теории линейных систем обыкновенных дифференциальных уравнений, М., 1957; Фрезер Р. А., Дункан В., Коллар А., Теория матриц и её приложения к дифференциальным уравнениям и динамике, перевод с английского, М., 1950; Вазов В., Форсайт Дж., Разностные методы решения дифференциальных уравнений в частных производных, перевод с английского, М., 1963.
В. Н. Фаддеева.
Значения в других словарях
- матрица — -ы, ж. 1. тех. Углубленная металлическая форма, применяемая при обработке металла давлением, при отливке типографских литер и пр. Линотипная матрица. 2. типогр. Обратная (углубленная) копия, снимаемая с набора на картоне, свинце, пластмассе и т. Малый академический словарь
- МАТРИЦА — 1. Сменный элемент литейной формы с углубленным рельефным изображением, использ. в полиграфии. 2. Углубленный оттиск с рельефной печатной формы на пластичном материале для получения копий этой печатной формы. М. широко использ. при изготовлении знаков почт, оплаты. Филателистический словарь
- Матрица — Прямоугольная таблица состоящая из тстрок и n столбцов, элементы к-рой принадлежат нек-рому множеству К. Таблица (1) наз. также -матрицей над К, или мат- рицей размера над K. Пусть — совокупность всех -матриц над К. Если т=п, то (1) наз. Математическая энциклопедия
- МАТРИЦА — МАТРИЦА. см. ДАННЫХ МАТРИЦА Социологический словарь
- матрица — 1) в металлообработке – одна из основных частей некоторых штампов или других рабочих инструментов со сквозным отверстием или углублением (соответствующим по форме или по контуру обрабатываемой детали). Техника. Современная энциклопедия
- матрица — Ма́триц/а. Морфемно-орфографический словарь
- матрица — орф. матрица, -ы, тв. -ей Орфографический словарь Лопатина
- матрица — Немецкое – Matrize. Французское – matrice. Латинское – matrix (мать, основа). Термин «матрица» пришел в русский язык в XVIII в. из немецкого, а туда из латинского через французский. Производное: матричный. Этимологический словарь Семёнова
- матрица — МАТРИЦА ы, ж., МАТРИС matrice f., нем. Matrize <�лат. matris. 1. Форма, в которой отливают буквы, знаки при книгопечатании. Сл. 18. Словарь галлицизмов русского языка
- Матрица — (нем. Matrize, от лат. matrix — матка, источник, начало) основная часть штампа для холодной и горячей штамповки, имеющая конфигурацию обрабатываемого предмета. М. пломбира — одна из его основных частей, крепящаяся на его коротких рычагах. Криминалистическая энциклопедия
- матрица — Заимств. в XVIII в. из нем. яз., где Matrize < франц. matrice, восходящего к лат. matrix, род. п. matricis «основа» < «мать», суф. производного от mater «мать». См. материк. Этимологический словарь Шанского
- Матрица — (нем. Matrize) в стоматологии — пластинка для временного замещения отсутствующей стенки зуба при его пломбировании. Медицинская энциклопедия
- МАТРИЦА — МАТРИЦА, прямоугольная таблица цифр, размещенных в ряды и колонки. Количество строк может не быть равно количеству столбцов. При помощи матриц, пользуясь определенными правилами, можно складывать, отнимать и умножать. Научно-технический словарь
- матрица — Выпуклая копия штампа для конгревного тиснения, имеющая достаточную прочность и жесткость. В процессе тиснения размещается на нижней плите пресса против штампа. Толковый словарь по полиграфии
- матрица — МАТРИЦА -ы; ж. [от лат. matrix (matricis) — матка] 1. Техн. Углублённая металлическая форма, применяемая при отливке металла под давлением, при отливке типографских литер и т.п. Линотипная м. 2. Типогр. Толковый словарь Кузнецова
- матрица — МАТРИЦА, ы, ж. (спец.). 1. Зеркальная копия печатной формы, служащая для отливки стереотипов. Картонная, пластмассовая, свинцовая м. 2. Таблица какихн. математических элементов, состоящая из строк и столбцов. Толковый словарь Ожегова
- матрица — Матрицы, ж. [нем. Matrize] (тех.). 1. Пластинка с выдавленными, вырезанными обратными знаками или изображениями чего-н., служащая формой для отливки или штамповки. С матриц отливают типографские литеры. Матрицы употребляются при чеканке монеты. Большой словарь иностранных слов
- матрица — М’АТРИЦА, матрицы, ·жен. (·нем. Matrize) (тех.). 1. Пластинка с выдавленными, вырезанными обратными знаками или изображениями чего-нибудь, служащая формой для отливки или штамповки. С матриц отливают типографские литеры. Толковый словарь Ушакова
- Матрица — Вогнутая часть формы, в которой пластическое тело формуется давлением (см. Медальерное дело). В частности медная пластинка с углубленным отпечатком, служащая для получения типографского шрифта; см. Словолитное дело. Энциклопедический словарь Брокгауза и Ефрона
- матрица — матрица I ж. Углубленная металлическая форма, применяемая при отливке металла под давлением, при отливке типографских литер и т.п. (в технике). II ж. Обратная — углубленная — копия, снимаемая с набора на картоне, свинце, пластмассе и т.п. Толковый словарь Ефремовой
- МАТРИЦА — МАТРИЦА — в металлообработке — инструмент со сквозным отверстием (реже углублением) — используемый при штамповке, прессовании и волочении для выдавливания, свертки или протягивания заготовки. Большой энциклопедический словарь
- матрица — ма́три́ца Через нов.-в.-н. Мatrize из франц. matrice от лат. mātrīх "матка". Этимологический словарь Макса Фасмера
- матрица — МАТРИЦА ж. изложница, льяло, льяк, гнездо, форма для отливки печатальных букв. Матрицовый или матричный, относящийся к матрице. Толковый словарь Даля
