ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ
Физическая теория, рассматривающая пространственно-временные закономерности, справедливые для любых физ. процессов. Универсальность пространственно-временных св-в, рассматриваемых О. т., позволяет говорить о них просто как о .св-вах пространства-времени. Наиболее общая теория пространства-времени наз. общей теорией относительности (ОТО) или теорией тяготения, т. к. согласно этой теории св-ва пространства-времени в данной области определяются действующими в ней полями тяготения. В излагаемой ниже частной теории относительности, основы к-рой были даны А. Эйнштейном в 1905, изучаются св-ва пространства-времени, справедливые с той точностью, с какой можно пренебрегать действием тяготения. Т. о., логически частная О. т. есть частный случай ОТО; исторически построение ОТО было завершено Эйнштейном позже (в 1915), после чего и появился термин «частная О. т.». В рус. литературе последняя наз. также специальной О.т. (что соответствует букв. переводу нем. слова speziell —.специальный, частный) или просто О. т.
Основные черты О. т. Явления, описываемые О. т., наз. релятивистскими (от лат. relativus — относительный) и проявляются при скоростях движения тел, близких к скорости света в вакууме с=2,99792458(1,2)X 1010 см/с. При таких скоростях (их принято называть релятивистскими) зависимость энергии ? тела от его скорости v описывается уже не ф-лой классич. механики
?кин = mv2/2, а релятив. ф-лой
?=mc2/?(1-v2/с2 ). (1) Масса т, входящая в эту ф-лу, наз. также массой покоя тела. Из (1) видно, что энергия тела стремится к бесконечности при v ®с, поэтому, если m?0, скорость тела всегда меньше с, хотя при ?->mс2 она может стать сколь угодно близкой к ней. Это наблюдается, напр., в опытах на ускорителях заряж. ч-ц, в к-рых ч-цам сообщаются энергии, много большие mc2, и они поэтому движутся со скоростью, практически равной с. Со скоростью света всегда движутся ч-цы, масса покоя к-рых равна нулю (фотоны, возможно, нейтрино). Скорость с явл. предельной скоростью передачи любых вэ-ствий и сигналов из одной точки пр-ва в другую.
Существование предельной скорости означает необходимость глубокого изменения обычных пространственно-временных представлений, основанных на повседневном опыте. Рассмотрим след. мысленный опыт. В вагоне, движущемся со скоростью v относительно полотна железной дороги, посылается световой сигнал в направлении движения. Скорость сигнала для наблюдателя в вагоне равна с. Если бы длины и промежутки времени, измеряемые любым наблюдателем, были одинаковы, то выполнялся бы закон сложения скоростей классич. механики, и для наблюдателя, стоящего у железнодорожного полотна, скорость сигнала была бы равна c+v, т. е. больше предельной. Противоречие устраняется тем, что для наблюдателя, относительно к-рого физ. система движется со скоростью v, все процессы в этой системе замедляются в 1/?(1-v2/c2) раз (это явление наз. замедлением времени), а продольные (вдоль движения) размеры тел во столько же раз сокращаются, и события, одновременные для одного наблюдателя, оказываются неодновременными для другого, движущегося относительно первого (т. н. о т н о с и т е л ь н о с т ь о д н о в р е м е н н о с т и). Учёт этих эффектов приводит к закону сложения скоростей, при к-ром предельная скорость одинакова для всех наблюдателей (см. ниже).
Характерное для О. т. явление замедления времени наблюдается при распадах нестабильных элем. ч-ц косм. лучей или получаемых с помощью ускорителей высоких энергий. Такие ч-цы движутся со скоростями, близкими к с, и, с точки зрения земного наблюдателя, их времена жизни, а следовательно, и проходимые ими от рождения до распада расстояния увеличиваются в тысячи и десятки тысяч раз.
Из релятив. ф-лы для энергии следует, что при малых скоростях (v<- с) энергия . тела равна: ?=mc2+mv2/2. Второй член справа есть обычная кинетич. энергия, первый же член показывает, что покоящееся тело обладает запасом энергии ?0=mc2, наз. э н е р г и е й п о к о я (т. н. принцип эквивалентности энергии и массы, или принцип эквивалентности Эйнштейна). В яд. реакциях и процессах превращений элем. ч-ц значит. часть энергии покоя может переходить в кинетич. энергию ч-ц. Так, источником энергии, излучаемой Солнцем, явл. превращение четырёх протонов в ядро гелия; масса ядра гелия меньше массы четырёх протонов на 5•10-26 г, поэтому при каждом таком превращении выделяется 4,5•10-5 эрг энергии, уносимой излучением. За счёт излучения Солнце теряет в 1 с 4•109кг своей массы.
О. т. подтверждена обширной совокупностью фактов и лежит в основе всех совр. теорий, рассматривающих явления при релятив. скоростях.
Принцип относительности и другие принципы инвариантности. Возникновение частной О. т. В основе О. т. лежит принцип относительности, согласно к-рому в физ. системе, приведённой в состояние свободного равномерного и прямолинейного движения относительно системы, условно наз. «покоящейся», для наблюдателя, движущегося вместе с системой, все процессы происходят в точности так же, как в покоящейся системе. Этот факт формулируют в виде утверждения об инвариантности законов природы относительно преобразований движения. Термин «принцип относительности» связан с тем, что если преобразованию движения подвергнуть систему движущихся тел, то все относительные движения этих тел останутся неизменными.
Наряду с принципом относительности из опыта известны и др. принципы инвариантности, или симметрии, законов природы. Любой физ. процесс происходит точно так же,
1) если осуществить его в любой др. точке пр-ва; эта симметрия выражает равноправие всех точек пр-ва, однородность пр-ва;
2) если систему, в к-рой происходит процесс, повернуть на произвольный угол; эта симметрия выражает равноправие всех направлений в пр-ве, изотропию пр-ва; 3) если повторить процесс через нек-рый произвольный промежуток времени; эта симметрия выражает однородность времени.
Т. о., имеет место инвариантность законов природы по отношению к четырём типам преобразований: 1) переносу в пр-ве,
2) вращению в пр-ве,
3) сдвигу во времени,
4) преобразованию движения.
Симметрии 1—4 выполняются точно только в изолированной от внеш. воздействий системе, т. е. если можно пренебречь воздействием на систему внеш. факторов; для реальных систем они справедливы лишь приближённо.
Изучение св-в преобразований 1, 2 составляет предмет евклидовой геометрии трёхмерного пр-ва, если рассматривать её как физ. теорию, описывающую св-ва физ. объектов (при этом под переносом следует понимать преобразование параллельного переноса).
При скоростях тел v, сравнимых с с, обнаруживается тесная связь и матем. аналогия между преобразованиями 1, 3 и 2, 4. Это даёт основание говорить об О. т., в к-рой все преобразования 1—4 следует рассматривать совместно, как о геометрии пространства-времени. Содержанием О. т. явл. рассмотрение св-в преобразований 1—4 и следствий из соответствующих принципов инвариантности. Математически О. т. явл. обобщением геометрии Евклида — геометрией четырёхмерного Минковского пространства-времени.
Принцип относительности был известен (и справедлив) в классич. механике, но св-ва преобразований движения при v<- с и при v = с различны; при v<-с релятив. эффекты исчезают и преобразования движения переходят в преобразования Галилея, справедливые для классич. механики (см. ГАЛИЛЕЯ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ).
Осн. понятие О. т.— точечное событие, т.е. нечто, происходящее в данной точке пр-ва в данный момент времени (напр., выстрел, распад элем. ч-цы). Это понятие явл. абстракцией — реальные события всегда имеют нек-рую протяжённость в пр-ве и во времени и могут рассматриваться как точечные только приближённо. Любой физ. процесс есть последовательность событий (С): C1, C2, . . ., Сn, . . . Справедливость симметрии 1—4 означает, что наряду с последовательностью (С) законы природы допускают существование бесконечного числа др. последовательностей (С), к-рые получаются из (С) соответствующим преобразованием и различаются положением событий в пр-ве и времени, но имеют одинаковую с (С) внутр. структуру. Напр., в случае симметрии 4 можно наглядно описать процесс (С) как происходящий в стоящем на земле самолёте, а процесс (С) как такой же процесс, происходящий в самолёте, летящем с пост. скоростью (относительно земли); разл. скоростям и направлениям движения соответствуют разл. последовательности (С). Преобразования, переводящие одну последовательность событий в другую, наз. активными (в отличие от п а с с и в н ы х преобразований, к-рые связывают координаты одного и того же события в двух системах координат; см. ниже). Совокупность всех возможных преобразований (1—4) с матем. точки зрения должны составлять группу; она наз. группой Пуанкаре. Преобразования группы Пуанкаре носят универс. хар-р: они действуют одинаково на события любого типа. Это позволяет считать, что они описывают св-ва пространства-времени, а не св-ва конкретных процессов. Преобразования Пуанкаре могут быть описаны разл. способами (так же, как можно описывать разл. способами движения в трёхмерном пр-ве); наиб. простое описание получается при использовании инерциальных систем отсчёта (и. с. о.) и связанных с ними часов. Роль и. с. о. в О. т. такая же, как роль прямоугольных декартовых координат в геометрии Евклида.
Осознание универс. справедливости принципа относительности для любых физ. явлений — результат сложного историч. развития. В 19 в. считалось, что принцип относительности справедлив только в механике, но несправедлив в оптике и в электродинамике, т. к. представлялось очевидным, что эл.-магн. волны (в т. ч. свет) — это волны в особой среде — эфире, заполняющем всё пр-во и определяющем привилегированную систему отсчёта, покоящуюся относительно эфира, в к-рой только и справедливы законы оптики и ур-ния электродинамики. Казалось очевидным, что в системе тел, движущейся относительно эфира, оптич. и эл.-магн. явления будут происходить иначе, чем в неподвижной, но все попытки обнаружить явление такого рода, предпринимавшиеся в 19 в. и в нач. 20 в., потерпели неудачу. Объяснение неудач искали, начиная с франц. физика О. Ж. Френеля, в динамике: используя конкретные динамич. законы, сформулированные в системе покоя эфира, показывали, что в данной системе тел эффекты, связанные с движением относительно эфира, компенсируются. Эта программа нашла известное завершение в работах голл. физика X. Лоренца и франц. математика А. Пуанкаре (1904—05), где было показано, что если принять лоренцовский вариант электродинамики эл-нов и предложенную Пуанкаре модель :эл-на, сжимаемого пост. давлением эфира, то компенсация будет точной и принцип относительности, понимаемый как невозможность обнаружения движения относительно эфира, выполняется. В 1905 в работе Пуанкаре были исследованы групповые св-ва преобразований движения и преобразований вращения с точки зрения наблюдателя, покоящегося относительно эфира. Переход к совр. точке зрения, согласно к-рой в абсолютно пустом пр-ве нельзя определить покоящуюся систему отсчёта и все связанные преобразованиями движения и . с. о. равноправны, был сделан Эйнштейном в 1905. В его работе была развита последоват. теория измерений времени и координат в и. с. о. и обнаружен относит. хар-р релятив. замедления времени и сокращения масштабов. Матем. аппарат теории в полной форме был развит нем. учёным Г. Минковским в 1908.
Инерциальные системы отсчёта. С той степенью точности, с какой св-ва данной области пространства-времени описываются частной О. т., можно ввести и. с. о., в к-рых описание пространственно-временных закономерностей О. т. принимает особенно простую форму. Под системой отсчёта в этом случае можно подразумевать жёсткую систему тв. тел (или её мысленное продолжение), по отношению к к-рой определяются положения событий, траектории тел и световых лучей. Любая система отсчета, движущаяся относительно данной и. с. о. равномерно и прямолинейно, без вращения, также будет инерциальной, а система отсчёта, вращающаяся или движущаяся ускоренно, уже не будет и. с. о. Таким образом, и. с. о. образуют выделенный класс систем отсчёта. В и. с. о. справедлив закон инерции, т. е. свободная ч-ца движется в и. с. о. прямолинейно и (при принятой синхронизации часов, см. ниже) равномерно. Требование выполнения закона инерции может быть принято как определение и. с. о. Первый закон Ньютона может рассматриваться при этом как утверждение о существовании таких систем отсчёта. Все и. с. о. равноправны, это равноправие явл. непосредств. выражением принципа относительности.
В области пространства-времени, в к-рой справедлива частная О. т., можно пользоваться и неинерц. системами отсчёта (так же, как можно пользоваться криволинейными координатами в геометрии Евклида), но при этом описание св-в пространства-времени оказывается более сложным.
В данной и. с. о. необходимо определить способ измерения времени и координат. В и. с. о. трёхмерная пространств. геометрия — евклидова, если прямые определить, напр., как траектории световых лучей, а расстояния измерять тв. масштабами. Поэтому в данной и. с. о. можно ввести декартовы прямоуг. координаты х, у, z. Для определения времени t события удобно представить, что в той точке, где оно произошло, находятся часы, покоящиеся в данной и. с. о. Если события происходят в разных точках А, В, то для сравнения их времён нужно синхронизировать часы в А и В, т. е. определить, что означает, что часы в А и В показывают одинаковое время. Обычное определение таково: пусть в момент tА по часам из А посылается сигнал в В, а в момент его прибытия в В посылается такой же сигнал из В в А ', если сигнал пришёл в Л в момент t'А , то принимается, что сигнал пришёл в 5 в момент tB=(tA+t'A)/2, и соотв. устанавливаются часы в В. При таком определении времена распространения сигнала из А в В и из В в А одинаковы и равны (T'А-TA)/2. Сигналами могут служить световые вспышки, звук. сигналы (если среда, в к-рой они распространяются, покоится по отношению к данной системе отсчёта), выстрелы из двух одинаковых орудий, установленных в А и В, и т. д., требуется лишь, чтобы условия передачи сигнала из А в A в и из В в А были одинаковыми. Целесообразность такого определения времени связана с тем, что в любой и. с. о. отсутствует к.-л. физически выделенное направление; описанная процедура синхронизации часов симметрична относительно А и В и поэтому не вносит анизотропии в способ описания. Отсутствие выделенного направления проявляется в том, что синхронизация любыми сигналами приводит к одному и тому же результату; к такому же результату приводит медленный (с v<-с) перенос часов из А в В. При практич. измерениях времён и координат используются многочисленные косвенные методы при условии, что они дают тот же результат, что и описанные выше процедуры. В любой другой и. с. о. координаты и время измеряются с помощью таких же масштабов и часов, синхронизируемых таким же способом. Заранее не очевидно, что времена, определённые таким методом в двух разл. и. с. о., будут одними и теми же, и они действительно оказываются различными. После того как синхронизация произведена, могут измеряться скорости ч-ц и сигналов в данной и. с. о., в частности скорость распространения световых сигналов. Скорость света в любой и. с. о. всегда равна с.
Преобразования Лоренца. Рассмотренные активные преобразования непосредственно связаны с пассивными преобразованиями, описывающими связь между координатами и временем данного события в двух разл. и. с. о. В силу принципа относительности безразлично, сообщить ли телу скорость V по отношению к данной и. с. о. L или перейти к системе отсчёта L', движущейся со скоростью V относительно L,— закон преобразования координат и времени должен быть одним и тем же.
В силу справедливости симметрии 1—4 преобразования, связывающие координаты и времена события х, у, z, t и x', у', z', t', измеренные в двух и. с. о. L и L', должны быть линейными. Из симметрии 1—4 и требования, чтобы преобразования составляли группу, можно получить вид этих преобразований. Если система отсчёта L' движется относительно L со скоростью V, то при надлежащем выборе осей координат и начал отсчёта времени в L и L' (оси х и х' направлены по V, оси у и y', z и z' соотв. параллельны, начала координат О и О' совпадают при t=0 и часы в L' установлены так, что при t=0 часы в О' показывают время t'=0) преобразования координат и времени имеют вид: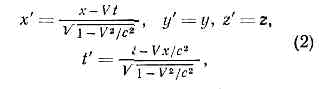
где с — параметр преобразования, имеющий смысл предельной скорости движения (равной скорости света в вакууме). Этот параметр может быть определён из любого эффекта О. т. (напр., из замедления времени распада быстрого p-мезона). Справедливость кинематики и динамики, основанных на преобразованиях (2), подтверждена неисчислимой совокупностью эксперим. фактов.
Преобразования Лоренца (2) вместе с преобразованиями вращения вокруг начала координат образуют г р у п п у Л о р е н ц а; добавление к ней сдвигов во времени t' =t+a и в пр-ве х'=х+b (где a, b — произвольные постоянные размерности времени и длины) даёт группу Пуанкаре.
Т. к. законы природы должны иметь одинаковую форму во всех и. с. о., они должны сохранять свой вид при преобразованиях Лоренца. Это требование наз. принципом (постулатом) р е л я т и в и с т с к о й и н в а р и а н т н о с т и, или л о р е н ц-и н в а р и а н т н о с т и (лоренц-ковариантности), законов природы.
Из преобразований Лоренца вытекает релятив. закон сложения скоростей. Если ч-ца или сигнал движется в L по оси х со скоростью v, то в момент t x=vt и в системе L' скорость ч-цы v' = x'lt' равна: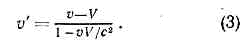
Из этой ф-лы видна осн. черта релятив. кинематики — независимость скорости света от движения источника. Действительно, если скорость света, испущенного покоящимся в нек-рой и. с. о. L источником, есть с, v=c, то из (3) получим, что в и. с. о. L' скорость света v' также равна с. Т. к. направление оси произвольно, то отсюда следует независимость скорости света от движения источника. Это св-во скорости света однозначно определяет вид преобразований Лоренца: постулировав независимость скорости света от движения источника, однородность пр-ва и времени и изотропию пр-ва, можно вывести преобразования Лоренца.
Из преобразований Лоренца легко получить осн. эффекты О. т.: относительность одновременности, замедление времени, сокращение продольных размеров движущихся тел. Действительно, события 1, 2, одновременные в одной и. с. о. L, t1=t2, оказываются неодновременными в другой и. с. о. L', t'2-t'1=(x1-x2)V!c2?(1-V2/c2)?0. Далее, когда часы, покоящиеся в L в точке x=0, показывают время t, то время t' по часам в L', пространственно совпадающим с часами в L в этот момент времени, есть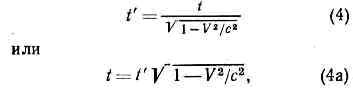
т. е., с точки зрения наблюдателя в L', часы в L отстают. В силу принципа относительности, с точки зрения наблюдателя в L', все процессы в L замедлены в такое же число раз.
Легко получить также, что размеры l всех тел, покоящихся в L, оказываются при измерении в L' сокращёнными в 1/?(1-V2/c2)раз в направлении V: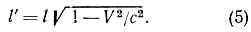
В частности, продольный диаметр сферы, движущейся со скоростью v относительно L, при измерении в L' будет в 1/?(1-v2/c2) раз короче, чем поперечный. (Заметим, что это сокращение не обнаружилось бы на мгновенной фотографии сферы: из-за разл. запаздывания световых сигналов, приходящих от разных точек сферы, её видимая форма остаётся прежней.)
Для и. с. о. пространственно-временные эффекты, определяемые преобразованиями Лоренца, относительны: с точки зрения наблюдателя в L, замедляются все процессы и сокращаются все продольные масштабы в L'. .Однако это утверждение несправедливо, если хотя бы одна из систем отсчёта неинерциальна. Если, напр., часы 1 перемещаются относительно L из А в В со скоростью v, а потом из В в А со скоростью -v, то часы 1 отстанут по сравнению с часами 2, покоящимися в A, в 1/?(1-v2/c2) раз; это можно обнаружить прямым сравнением, так что эффект абсолютен. Он должен иметь место для любого процесса; напр., близнец, совершивший путешествие со скоростью v, вернётся в 1/?(1-v2/с2) раз более молодым, чем его брат, остававшийся неподвижным в и. с. о. Это явление, получившее назв. парадокса близнецов, в действительности не содержит парадокса: система отсчёта, связанная с часами 1, не явл. инерциальной, т. е. эти часы испытывают ускорение при повороте в В по отношению к инерц. системе; поэтому часы 1 и 2 н е р а в н о п р а в н ы.
При малых скоростях v преобразования Лоренца переходят в преобразования Галилея х'=х-vt, y'=y, z' = z, t'=t, к-рые описывают связь между картинами разл. наблюдателей, известную из повседневного опыта: размеры предметов и длительность процессов одинаковы для всех наблюдателей.
Преобразования Пуанкаре оставляют инвариантной величину, наз. интервалом sAB между событиями А и В, к-рый определяется соотношением: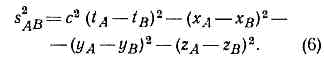
Математически инвариантность s аналогична инвариантности расстояния при преобразованиях движения в евклидовой геометрии. Величины ct, x, у, z можно рассматривать как четыре координаты события в четырёхмерном пространстве-времени Минковского: x0=ct. xl=x, x2=y, x3=z,
к-рые явл. компонентами четырёхмерного вектора.
С матем. точки зрения частная О. т. есть геометрия пространства-времени Минковского. (Если вместо х0 ввести мнимую координату x4=ix0=ict, то произвольное преобразование Пуанкаре можно записать в виде, полностью аналогичном ф-ле, описывающей вращения и сдвиги в трёхмерном пр-ве.) Вследствие того, что квадраты разностей временных и пространств. координат входят в (6) с разными знаками, знак s2 может быть различным, геометрия такого пр-ва отличается от евклидовой и наз. п с е в д о е в к л и д о в о й.
Законы сохранения в О. т. и релятивистская механика. В О. т., так же как в классич. механике, для замкнутой физ. системы сохраняется импульс р и энергия ?. Трёхмерный вектор импульса вместе с энергией образует четырёхмерный вектор энергии-импульса с компонентами ?/с, р. При преобразованиях Лоренца остаётся инвариантной величина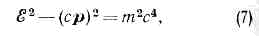
где т — масса покоя ч-цы. Из требований лоренц-инвариантиости следует, что зависимость энергии и импульса от скорости имеет вид: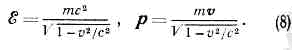
Энергия и импульс ч-цы связаны соотношением p=?v/c2. Оно справедливо также для ч-цы с нулевой массой покоя; тогда v=c и р=?/с.
Обсуждалась возможность существования объектов, движущихся со скоростью, большей скорости света в вакууме (т. н. тахионов). Формально это не противоречит лоренц-пнварнантности, но приводит к серьёзный затруднениям с выполнением принципа причинности.
Масса покоя т не явл. сохраняющейся величиной. В частности, в процессах распадов и превращений элем. ч-ц сумма энергий и импульсов ч-ц сохраняется, а сумма масс покоя меняется. Так, в процессе аннигиляции позитрона и эл-на в два фотона, е++е-®2g, сумма масс покоя изменяется на 2mе (mе — масса покоя эл-на).
В системе отсчёта, в к-рой тело покоится (такая система отсчёта наз. с о б с т в е н н о й), его энергия (энергия покоя) есть ?0=mс2. Если тело, оставаясь в покое, изменяет своё состояние, получая энергию в виде излучения или тепла, то из релятив. закона сохранения энергии следует, что полученная телом энергия D? связана с увеличением его массы покоя соотношением D?=Dmс2. Величина ?0=mс2 определяет макс. величину энергии, к-рая может быть «извлечена» из данного тела в системе отсчёта, в к-рой оно покоится.
Для движущегося тела величина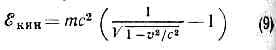
определяет его кинетич. энергию. При v<-с (9) переходит в нерелятив. выражение ?кин=mv2/2, при этом импульс p=mv. Из определения ?кин следует, что для любого процесса в изолированной системе выполняется равенство:
D(S?кин) = -с2D(Sm). (10)
согласно к-рому увеличение кинетич. энергии пропорц. уменьшению суммы масс покоя. Это соотношение широко используется в яд. физике; оно позволяет предсказывать энерговыделение в яд. реакциях, если известны массы покоя участвующих в них ч-ц. Возможность протекания процессов, в к-рых происходит превращение энергии покоя в кинетич. энергию ч-ц, ограничена др. законами сохранения (напр., законом сохранения барионного заряда, запрещающим процесс превращения протона в позитрон и g-квант). Иногда вводят массу, определяемую как
mдвиж=m/?(1-v2/c2) (11)
При этом связь между импульсом и скоростью приобретает тот же вид, что и в ньютоновской механике: р=mдвижv. Так определ. масса отличается от энергии тела лишь множителем 1/с2. (В теор. физике часто выбирают ед. измерения, полагая с=1, тогда ?=m.)
Осн. ур-ния релятив. механики имеют такой же вид, как и второй закон Ньютона и ур-ние энергии, только вместо нерелятив. выражений для энергии и импульса используются выражения (8):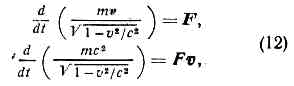
где F — сила, действующая на тело. Для заряж. ч-цы, движущейся в эл.-магн. поле, F есть Лоренца, сила.
О. т. и эксперимент. Предположения о точечных событиях (означающее локальность вз-ствий), о справедливости принципа относительности, однородности времени и однородности и изотропии пр-ва с неизбежностью приводят к О. т. При этом абстрактно допустим предельный случай, соответствующий с=?, однако такая возможность исключается экспериментом: доказано, что предельная скорость с есть скорость света в вакууме.
Каковы границы применимости О. т.? Отклонения от пространственно-временной геометрии О. т., связанные с гравитацией, наблюдаемы и рассчитываются в ОТО; никаких других ограничений применимости О. т. не обнаружено, хотя неоднократно высказывались предположения, что на очень малых расстояниях (напр., =10-17 см) понятие точечного события, а следовательно, и О. т. могут оказаться неприменимыми (см. КВАНТОВАНИЕ ПРОСТРАНСТВА-ВРЕМЕНИ). Совр. квант. теории фундам. вз-ствий (эл.-магн., слабого, сильного) целиком основаны на геометрии пространства-времени частной О. т. Из этих теорий с наиб. высокой точностью проверена квант. электродинамика лептонов, применимость к-рой установлена до расстояний 10-16 см. Отсюда следует, что по крайней мере до этих расстояний действует геометрия частной О. т. Неоднократно повторялись с высокой точностью классич. опыты, использовавшиеся для обоснования О. т. в первые десятилетия её существования (Майкельсона опыт и др.). Такого рода опыты сейчас представляют в основном историч. интерес, т. к. осн. массив подтверждений ОТО составляют данные, относящиеся к вз-ствиям релятив. элем. ч-ц, где справедливость кинематики частной О. т. проверена на обширном материале.
Значения в других словарях
- Относительности Теория — Физическая теория, рассматривающая пространственно-временные свойства физич. процессов. Эти свойства являются общими для всех физич. процессов, поэтому их часто наз. просто свойствами пространства-времени. Математическая энциклопедия
- Относительности теория — Физическая теория, рассматривающая пространственно-временные свойства физических процессов. Закономерности, устанавливаемые О. т., являются общими для всех физических процессов, поэтому часто о них говорят просто как о свойствах пространства-времени. Большая советская энциклопедия
- ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ — ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ — физическая теория пространства и времени. В частной (специальной) теории относительности рассматриваются только инерциальные системы отсчета. Большой энциклопедический словарь
