ГАЛИЛЕЯ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ

Принцип физ. равноправия всех инерциальных систем отсчёта (и. с. о.) в классич. механике, проявляющегося в том, что законы механики во всех таких системах одинаковы. Отсюда следует, что никакими механич. опытами, проводящимися в какой-либо и. с. о., нельзя определить, покоится данная система или движется равномерно и прямолинейно. Это положение было впервые установлено итал. учёным Г. Галилеем в 1636.

Движение матер. точки относительно: её положение, скорость, вид траектории зависят от того, по отношению к какой и. с. о. (телу отсчёта) это движение рассматривается. В то же время законы классич. механики одинаковы .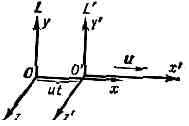

Инерц. система отсчёта L' движется относительно другой инерц. системы отсчёта L в направлении оси х с пост. скоростью u. Координатные оси выбраны так, что в нач. момент времени (t=0) соответствующие оси координат совпадают в обеих системах.

во всех и. с. о. Относительность мехаиич. движения и одинаковость законов механики в разных и. с. о. и составляют содержание Г. п. о. Математически Г. п. о. выражает инвариантность ур-ний механики относительно преобразований координат движущихся точек (и времени) при переходе от одной и. с. о. к другой — преобразования Галилея. Для двух и. с. о.— L и L', движущейся по отношению к L с пост. скоростью и так, как показано на рисунке, преобразования Галилея для координат матер. точки и времени t будут иметь вид:

х'=х-ut, y'=y, z'=z: t'=t (1)

(штрихованные величины относятся к системе L', нештрихованные — к L). Т. о., время в классич. механике, как и расстояние между любыми фиксиров. точками, считается одинаковым во всех системах отсчёта. Из (1) можно получить соотношения между скоростями движения точки и её ускорениями в обеих и. с. о.:

v'=v-и, (2) а'=а.

В классич. механике движение матер. точки (массы т) определяется вторым законом Ньютона:

F=ma, (3)

где F — равнодействующая всех приложенных к ней сил. При этом силы (и массы) явл. инвариантными (не изменяются при переходе от одной системы отсчёта к другой). Поэтому при преобразованиях Галилея ур-ние (3) не меняется. Это и есть матем. выражение Г. п. о.

Г. п. о. справедлив лишь в случае движения тел со скоростями, много меньшими скорости света. При v=c преобразования (1) должны быть заменены преобразованиями Лоренца (см. ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ).