адсорбция
АДСОРБЦИЯ (от лат. ad — на, при и sorbeo — поглощаю)
изменение (обычно-повышение) концентрации вещества вблизи поверхности раздела фаз ("поглощение на поверхности"). В общем случае причина А. — нескомпенсированность межмол. сил вблизи этой поверхности, т. е. наличие адсорбц. силового поля. Тело, создающее такое поле, наз. адсорбентом, вещество, молекулы которого могут адсорбироваться,-а д с о р б т и в о м, уже адсорбиров. вещество-адсорбатом. Процесс, обратный А., наз. десорбцией.
Природа адсорбц. сил м. б. весьма различной. Если это ван-дер-ваальсовы силы, то А. наз. физической, если валентные (т. е. А. сопровождается образованием поверхностных хим. соединений), — химической, или хемосорбцией. Отличит. черты хемосорбции — необратимость, высокие тепловые эффекты (сотни кДж/моль), активированный характер. Между физ. и хим. А. существует множество промежут. случаев (напр., А., обусловленная образованием водородных связей). Возможны также разл. типы физ. А. наиб. универсально проявление дисперсионных межмол. сил притяжения, т. к. они приблизительно постоянны для адсорбентов с поверхностью любой хим. природы (т. наз. неспецифич. А.). Физ. А. может быть вызвана электростатич. силами (взаимод. между ионами, диполями или квадруполями); при этом А. определяется хим. природой молекул адсорбтива (т. наз. специфич. А.). значит. роль при А. играет также геометрия поверхности раздела: в случае плоской поверхности говорят об А. на открытой поверхности, в случае слабо или сильно искривленной поверхности-об А. в порах адсорбента.
В теории А. различают статику (система адсорбент-адсорбат находится в термодинамич. равновесии) и кинетику (равновесия нет).
Статика адсорбции
Термодинамика. Основы термодинамики А. были созданы Дж. Гиббсом в 70-е гг. 19 в. По Гиббсу, в равновесной двухфазной системе вблизи поверхности раздела фаз происходит некоторое изменение локальных значений всех экстенсивных свойств (кроме объема). Однако фазы считаются однородными вплоть до некоторой геом. поверхности, разделяющей их. Поэтому значение к.-л. экстенсивного свойства для системы в целом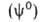 не равно сумме значений этого свойства в однородных фазах α и
не равно сумме значений этого свойства в однородных фазах α и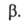 Разность
Разность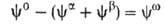 приписывается двухмерной поверхностной фазе, связанной с разделяющей поверхностью. Т. к. поверхностная фаза не имеет толщины, то V0 =
приписывается двухмерной поверхностной фазе, связанной с разделяющей поверхностью. Т. к. поверхностная фаза не имеет толщины, то V0 =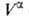 +
+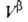 и
и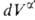 = —
= —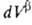 , где V — объем.
, где V — объем.
Изложенные представления позволяют привести фундам. термодинамич. уравнение к виду:
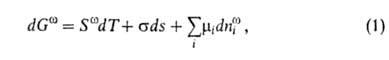
где G-гиббсова своб. энергия, 5-энтропия, σ-межфазное поверхностное натяжение, 5-площадь поверхности раздела, 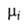 и иi- — соотв. хим. потенциал и число молей i-того компонента. Индекс
и иi- — соотв. хим. потенциал и число молей i-того компонента. Индекс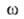 указывает на значение соответствующего свойства в поверхностной фазе. Преобразование Лежандра позволяет видоизменить уравнение (1) для изотермич. условий:
указывает на значение соответствующего свойства в поверхностной фазе. Преобразование Лежандра позволяет видоизменить уравнение (1) для изотермич. условий:
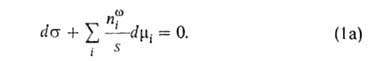
Величина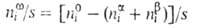 наз. гиббсовой А. и обозначается символом Г, (выражается в моль/см2). Для двух-компонентной системы:
наз. гиббсовой А. и обозначается символом Г, (выражается в моль/см2). Для двух-компонентной системы:
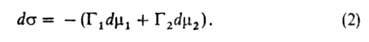
Положение разделяющей поверхности м. б. выбрано произвольно. В частности, выбор этого положения может удовлетворять условию Г1 = 0. Такая поверхность наз. эквимолекулярной. Для нее вводится обозначение Г2 = Г2(1) Отсюда следует осн. адсорбц. уравнение Гиббса:

Если адсорбтив совершенно не раств. в одной из двух фаз, 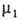 = const, и переход от уравнения (2) к уравнению (3) не требует условия Г1 = 0. Таким образом, гиббсова А.-это избыток данного компонента в реальной двухфазной системе по сравнению с такой системой, в которой обе фазы были бы строго однородны вплоть до разделяющей поверхности. Кроме гиббсовых избыточных величин А., в ее теории большую роль играет А., понимаемая как полное содержание компонента i в пространстве W, в котором проявляются адсорбц. силы. Обозначая полное содержание через а и считая, что компонент i совершенно не раств. в одной из объемных фаз, имеем:
= const, и переход от уравнения (2) к уравнению (3) не требует условия Г1 = 0. Таким образом, гиббсова А.-это избыток данного компонента в реальной двухфазной системе по сравнению с такой системой, в которой обе фазы были бы строго однородны вплоть до разделяющей поверхности. Кроме гиббсовых избыточных величин А., в ее теории большую роль играет А., понимаемая как полное содержание компонента i в пространстве W, в котором проявляются адсорбц. силы. Обозначая полное содержание через а и считая, что компонент i совершенно не раств. в одной из объемных фаз, имеем:

где ci-концентрация i-того компонента в объемной фазе. При малых сi:
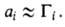
А. может происходить на любой поверхности раздела между двумя любыми фазами, в частности на поверхности раздела флюид-флюид (жидкость — газ, жидкость — жидкость) или твердое тело-флюид (твердое — газ, твердое-жидкость). В системах флюид-флюид можно измерить а как функцию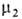 и экспериментально определить Г2(1) по уравнению (3). Во втором случае ппя определения Г2(1) измеряют любым методом ni0,
и экспериментально определить Г2(1) по уравнению (3). Во втором случае ппя определения Г2(1) измеряют любым методом ni0, 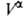 ,
, 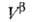 и концентрации i-того компонента в этих объемах. Отсюда вычисляют Гi(1) Этот метод наз. объемным (или волюмометрич.). При весовом (гравиметрии.) методе непосредственно определяют количество i-того компонента на поверхности раздела.
и концентрации i-того компонента в этих объемах. Отсюда вычисляют Гi(1) Этот метод наз. объемным (или волюмометрич.). При весовом (гравиметрии.) методе непосредственно определяют количество i-того компонента на поверхности раздела.
Изотерма адсорбции. В равновесной адсорбц. системе параметры, определяющие равновесие,-это ai парциальные давления р (или сi) и температура Т. Они связаны т. наз. термич. уравнением:
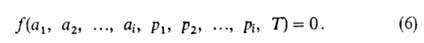
При А. индивидуального адсорбтива (i=1) это уравнение принимает вид:

Три частных случая термич. уравнения (когда Т, р или a-константы) играют особую роль в теории А.:
а=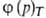 — уравнение изотермы А.,
— уравнение изотермы А.,
Т=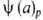 — уравнение изобары А.,
— уравнение изобары А.,
Р-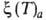 — уравнение изостеры А.
— уравнение изостеры А.
Конкретный вид функций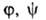 и
и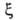 определяется особенностями рассматриваемой системы. Если одна из них, напр.
определяется особенностями рассматриваемой системы. Если одна из них, напр.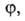 известна для любого значения Т= const, то, очевидно, становятся известными и две другие. При этом не обязательно, чтобы был известен аналит. вид зависимостей. Они м. б. заданы эмпирически в виде набора значений а, р и Т.
известна для любого значения Т= const, то, очевидно, становятся известными и две другие. При этом не обязательно, чтобы был известен аналит. вид зависимостей. Они м. б. заданы эмпирически в виде набора значений а, р и Т.
В теории А. обычно решается вопрос о виде функции а =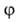 (р)г, т. е. об уравнении изотермы А. Эта проблема связана с тепловыми эффектами, сопровождающими А. При расчете изменения значений осн. термодинамич. функций в случае перехода dn молей адсорбтива из объемной фазы в поверхностную в равновесной системе при р = const возможны два случая: в первом учитывается только превращ. адсорбтива в адсорбат, поскольку адсорбент при А. термодинамически неизменен и его роль-служить источником адсорбц. поля; во втором учитывается и изменение адсорбента.
(р)г, т. е. об уравнении изотермы А. Эта проблема связана с тепловыми эффектами, сопровождающими А. При расчете изменения значений осн. термодинамич. функций в случае перехода dn молей адсорбтива из объемной фазы в поверхностную в равновесной системе при р = const возможны два случая: в первом учитывается только превращ. адсорбтива в адсорбат, поскольку адсорбент при А. термодинамически неизменен и его роль-служить источником адсорбц. поля; во втором учитывается и изменение адсорбента.
Т.к. система равновесна, то хим. потенциалы адсорбата и адсорбтива одинаковы; энтропия адсорбата вследствие уменьшения подвижности молекул при А. меньше энтропии адсорбтива. Поэтому при инертном адсорбенте энтальпия всегда отрицательна, т. е. А. экзотермична. Учет изменения энтропии адсорбента может изменить этот вывод. Например, при сорбции полимерами веществ, в которых полимер набухает, энтропия последнего (из-за увеличения подвижности макромолекул) может столь сильно возрасти, что А. становится эндотермической. В дальнейшем в статье рассматривается только экзотермич. А.
Различают интегральную, дифференц., изостерич. и среднюю теплоты А. Интегральная теплота Q равна убыли энтальпии (при V= const — внутр. энергии) при изменении А. от a1 до а2(в частном случае м. б. а1=0): Q= -(H2 — H1) Эту величину относят обычно к массе адсорбента и выражают в Дж/кг.
Дифференц. теплота q (Дж/моль) равна убыли энтальпии dH при изменении а на da. Ее выражают отношением q = — (dH/da). Очевидно, что
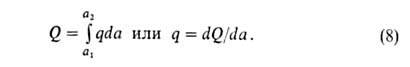
Изостерич. теплоту qst принимают равной:
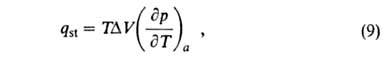
где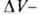 разность мольных объемов адсорбата и адсорбтива. Можно показать, что
разность мольных объемов адсорбата и адсорбтива. Можно показать, что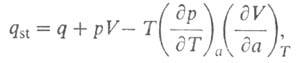 для идеального газового адсоритива:
для идеального газового адсоритива:

Смысл введения qsi в том, что для ее определения не требуется калориметрич. данных (таких, как Q и q) и она м. б. вычислена по уравнению (9) по результатам измерения А. Вводят также среднюю теплоту Q (Дж/моль):
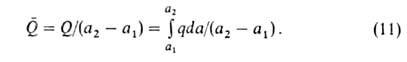
С ростом а параметр Q всегда возрастает, a q может уменьшаться, увеличиваться или оставаться неизменной. С ростом а при неоднородной поверхности А. происходит на все менее активных участках, что приводит к уменьшению q. Однако при этом уменьшаются средние расстояния между адсорбиров. молекулами, вследствие чего увеличиваются силы притяжения между ними, и q возрастает. Соотношение между двумя упомянутыми эффектами определяет ход зависимости q =f(a). При очень больших а начинают преобладать силы отталкивания и в этой области q всегда снижается с ростом а.
При очень малых заполнениях поверхности уравнение изотермы А. имеет вид уравнения Генри:
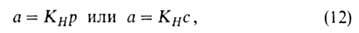
где KH-коэф. Генри. Действительно, при очень малых а адсорбц. слой подобен двухмерному идеальному газу, поэтому его уравнение состояния имеет вид: 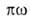 = RT, где
= RT, где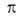 — двухмерное давление,
— двухмерное давление, 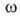 -площадь, занимаемая одним молем вещества. Отсюда, учитывая, что
-площадь, занимаемая одним молем вещества. Отсюда, учитывая, что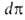 = —
= —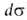 , и используя уравнение (3), получаем уравнение (12). Уравнение Генри требует, чтобы q было постоянным. При больших заполнениях это уравнение перестает выполняться. Поэтому Г. Фрейндлих (1906) предложил описывать изотермы А. след. эмпирич. уравнением (уравнение Фрёйндлиха ):
, и используя уравнение (3), получаем уравнение (12). Уравнение Генри требует, чтобы q было постоянным. При больших заполнениях это уравнение перестает выполняться. Поэтому Г. Фрейндлих (1906) предложил описывать изотермы А. след. эмпирич. уравнением (уравнение Фрёйндлиха ):

где k и п — константы. Этим уравнением часто пользуются как интерполяц. формулой, хотя оно при малых р не переходит в уравнение (12), а при очень больших р приводит к несогласующемуся с опытом неогранич. возрастанию а.
Строгая теория изотермы А. была создана И. Ленгмю-ром (1914–18). В основу теории положена след. модель: 1) поверхность адсорбента представляет собой набор энергетически одинаковых активных центров, на которых адсорбируются (локализуются) молекулы адсорбтива; 2) на одном центре адсорбируется только одна молекула, т. е. при А. образуется только один адсорбц. слой (монослой); 3) А. на данном центре не влияет на А. на др. центрах, т. е. взаимод. адсорбированных молекул можно пренебречь.
Модель Ленгмюра наз. локализованной мономолекулярной А. на однородной поверхности. Уравнение изотермы А., соответствующее этой модели, м. б. получено при помощи разл. методов (молекулярно-кинетич., термодинамич., ста-тистико-термодинамич.). Так, адсорбц. равновесие можно выразить след. схемой:
Молекула Своб. Адсорбц. в газовой + адсорбц. ⇄ комплекс фазе центр (занятый центр)
Концентрация молекул в газе пропорциональна р, концентрация своб. центров-величине (ат — а), где ат- полное число центров, а-число занятых центров, концентрация адсорбц. комплексов-величине а. Следовательно, константа равновесия равна: Kр = р(ат — а)/а. Отсюда получаем уравнение Ленгмюра:
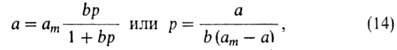
где b — т. наз. адсорбц. коэф., равный Kр−1. В области очень малых давлений bр " 1 и a = (amb)p, что отвечает уравнению Генри, в котором KH = amb. В области очень больших давлений bр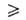 1 и а
1 и а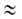 ат; при этом А. перестает зависеть от давления. Константа равновесия b−1связана со стандартным значением изобарного потенциала реакции:
ат; при этом А. перестает зависеть от давления. Константа равновесия b−1связана со стандартным значением изобарного потенциала реакции:
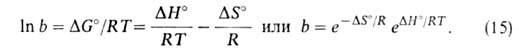
Модель Ленгмюра требует, чтобы дифференц. теплота и энтропия А. не зависели от степени заполнения поверхности.
Уравнение (14)-строгое выражение, соответствующее модели Ленгмюра, однако оно редко оправдывается на опыте, поскольку сама модель идеализирована. Учение об А. с 20-х гг. 20 в. в значит. степени строилось на основе ослабления или исключения того или иного допущения Ленгмюра.
Уже Ленгмюр предложил способ описания А. на неоднородной поверхности (т. е. при допущении, что не все центры оди наковы). Объединяя одинаковые центры в группы и полагая, что к каждой группе применимо уравнение (14), можно считать, что А. на всей поверхности выражается суммой членов уравнения (14):
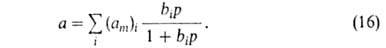
Полагая, что число адсорбц. центров м. б. описано непрерывной функцией распределения по значениям своб. энергии, Я.Б.Зельдович получил из формулы (16) для экспоненциальной функции уравнение типа (13).
А. на неоднородных поверхностях-большая глава теории А. Ее осн. задача-решение интегрального уравнения:
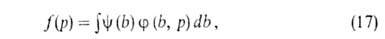
где f(р)- т. наз. эмпирич. изотерма А., 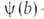 — та или иная функция распределения числа центров по значениям своб. энергии,
— та или иная функция распределения числа центров по значениям своб. энергии, 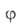 (b, р)- локальная изотерма А., в качестве которой обычно принимают изотерму Ленгмюра.
(b, р)- локальная изотерма А., в качестве которой обычно принимают изотерму Ленгмюра.
Много попыток сделано в направлении отказа от второго допущения Ленгмюра. На этом пути особое значение приобрела теория полимолекулярной А., предложенная С. Брунауэром, П. Эмметом и Э. Теллером (теория БЭТ). Теория постулирует, что при температуре ниже критической каждая молекула, адсорбированная в первом слое (теплота адсорбции qi,), является центром для молекул, образующих второй слой, и т. д. При этом считается, что теплота А. во всех слоях, кроме первого, равна теплоте конденсации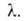 Такая модель приводит к уравнению:
Такая модель приводит к уравнению:
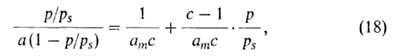
где с = ехр[(q1 -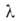 )/RT]. Уравнение (18) в координатах a, p/ps соответствует S-образной кривой. В координатах p/ps,
)/RT]. Уравнение (18) в координатах a, p/ps соответствует S-образной кривой. В координатах p/ps,
изотерма А. по уравнению (18) должна быть линейной.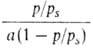 Наклон этой прямой (обычно в интервале 0,05 < p/ps < < 0,30) и отрезок, отсекаемый ею на оси ординат, дают значения соотв. ат и с. Широкое распространение теории БЭТ связано с тем, что ее авторы, фактически считая А. нелокализованной, отождествляют константу ат не с числом дискретных адсорбц. центров, а с числом молекул адсорба-та в первом слое при плотнейшей упаковке (при р = ps). Поэтому, вводя представление о площади
Наклон этой прямой (обычно в интервале 0,05 < p/ps < < 0,30) и отрезок, отсекаемый ею на оси ординат, дают значения соотв. ат и с. Широкое распространение теории БЭТ связано с тем, что ее авторы, фактически считая А. нелокализованной, отождествляют константу ат не с числом дискретных адсорбц. центров, а с числом молекул адсорба-та в первом слое при плотнейшей упаковке (при р = ps). Поэтому, вводя представление о площади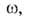 занимаемой одной молекулой в этом слое, принимают:
занимаемой одной молекулой в этом слое, принимают:

где s — площадь поверхности адсорбата. Как правило, для этого измеряют изотерму А. азота и принимают, что для его молекулы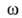 = 0,162нм2. Часто выполняемый аналогичный расчет s по модели Ленгмюра не корректен, т. к. этот метод, очевидно, применим только к нелокализованной А.
= 0,162нм2. Часто выполняемый аналогичный расчет s по модели Ленгмюра не корректен, т. к. этот метод, очевидно, применим только к нелокализованной А.
В теорию полимолекулярной А. большой вклад внес Я. де Бур, экспериментально показавший, что зависимость среднего числа слоев (свыше первого) на всех поверхностях, близких по хим. природе, от p/ps выражается универсальной кривой (т. наз. t-кривой). Это также позволяет оценивать площади поверхности адсорбтивов.
Предпринимались попытки учесть в модели Ленгмюра также взаимод. между адсорбиров. молекулами. Так, Т. Хилл и Я. де Бур, считая, что уравнение состояния адсорбц. слоя есть двухмерный аналог уравнения Ван-дер-Ваальса, получили след. уравнение изотермы А.:
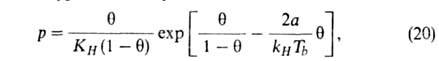
где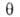 = а/ат, а и b-константы уравнения Ван-дер-Ваальса. Р. Фаулер и Э. Гуггенгейм, учтя взаимод. адсорбиров. молекул, вывели уравнение:
= а/ат, а и b-константы уравнения Ван-дер-Ваальса. Р. Фаулер и Э. Гуггенгейм, учтя взаимод. адсорбиров. молекул, вывели уравнение:
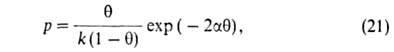
где α-константа, связанная с парным взаимодействием молекул.
Существует еще один механизм, приводящий к дополнит. А. адсорбтивов ниже их критич. температуры на пористых адсорбентах при сравнительно высоких значениях p/ps. Это — капиллярная конденсация. Если в поре образовался вогнутый мениск адсорбата, то в ней начинается конденсация при p/ps<1. Согласно уравнению Кельвина:
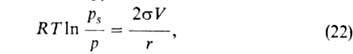
где σ-поверхностное натяжение адсорбата, V-его мольный объем, r-радиус кривизны мениска. Капиллярная конденсация приводит к резкому подъему изотермы А. При этом часто (но не всегда) наблюдается т. наз. адсорбц. гистерезис, т. е. несовпадение адсорбц. и десорбц. ветвей изотермы. Как правило, это связано с тем, что формы менисков при А. и десорбции не совпадают.
Капиллярную конденсацию используют для определения размеров пор адсорбента. По уравнению (22) для каждого значения p/ps вычисляют радиус кривизны мениска. Из него, учитывая толщину адсорбц. слоя (напр., по t-кривой), форму переходной области от слоя к мениску и зависимостьσ от кривизны при очень малых r, находят линейный размер (эффективный радиус ref) пор, заполняемых при данном p/ps. Объем таких пор определяют по приросту А. в этой точке изотермы. Используя полученные данные, строят кривую распределения объема пор по их радиусам. Метод применим при ref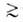 1,5 нм. Обычно расчет ведут по десорбц. ветви изотермы, но более строгая совр. теория требует для построения кривой учета обеих ветвей.
1,5 нм. Обычно расчет ведут по десорбц. ветви изотермы, но более строгая совр. теория требует для построения кривой учета обеих ветвей.
Потенциальная теория адсорбции и теория объемного заполнения микропор. Модель А., принципиально отличную от ленгмюровской, предложил в 1914 М. Поляки. Согласно этой модели, вблизи поверхности адсорбента существует потенциальное адсорбц. силовое поле, убывающее с расстоянием от поверхности. Вследствие этого давление адсорбтива, равное вдали от поверхности р, вблизи нее возрастает и на некотором расстоянии достигает значения ps, при котором адсорбтив конденсируется. Объем слоя между поверхностыо раздела и геом. местом точек, где р = ps, заполнен жидкостью, которой приписываются нормальные значения физ. свойств объемной жидкости. Обратимая изотермич. работа е адсорбц. сил, определяемая по уравнению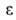 = RTlnp/ps, наз. адсорбц. потенциалом, а вся концепция-потенциальной теорией А. При заданной величине объема V адсорбц. слоя потенциал
= RTlnp/ps, наз. адсорбц. потенциалом, а вся концепция-потенциальной теорией А. При заданной величине объема V адсорбц. слоя потенциал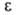 не зависит от температуры (вследствие независимости дисперсионных сил от температуры). Такая температурная инвариантность дает возможность пересчитывать А. с одной температуры на другую, хотя уравнения изотермы А. на основе излагаемой теории вывести не удавалось. Модель Поляни широко и успешно применялась мн. авторами, однако она содержала два очень уязвимых положения: 1) допущение о том, что тончайшая адсорбц. пленка имеет нормальные значения физ. свойств объемной жидкости (это допущение не подтверждалось опытами); 2) температурная инвариантность функции
не зависит от температуры (вследствие независимости дисперсионных сил от температуры). Такая температурная инвариантность дает возможность пересчитывать А. с одной температуры на другую, хотя уравнения изотермы А. на основе излагаемой теории вывести не удавалось. Модель Поляни широко и успешно применялась мн. авторами, однако она содержала два очень уязвимых положения: 1) допущение о том, что тончайшая адсорбц. пленка имеет нормальные значения физ. свойств объемной жидкости (это допущение не подтверждалось опытами); 2) температурная инвариантность функции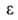 =f(V), лежащая в основе теории, приближенно подтверждалась опытом только для очень тонкопористых адсорбентов.
=f(V), лежащая в основе теории, приближенно подтверждалась опытом только для очень тонкопористых адсорбентов.
Используя потенциальную теорию, М.М. Дубинин предложил и разработал теорию объемного заполнения микро-пор (ТОЗМ). Было постулировано, что эта теория применима только к микропористым адсорбентам. Особенность таких адсорбентов, в которых линейные размеры пор r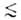 1 нм, состоит в том, что весь объем их пор "заполнен" адсорбц. полем. Поэтому при А. они заполняются не послойно, а объемно. Величина
1 нм, состоит в том, что весь объем их пор "заполнен" адсорбц. полем. Поэтому при А. они заполняются не послойно, а объемно. Величина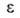 в рассматриваемом случае — это не адсорбц. потенциал, а с точностью до знака хим. потенциал адсорбата, отсчитываемый от уровня хим. потенциала нормальной жидкости при той же температуре. Вся совокупность пор адсорбентов разделяется на три класса: микропоры (r
в рассматриваемом случае — это не адсорбц. потенциал, а с точностью до знака хим. потенциал адсорбата, отсчитываемый от уровня хим. потенциала нормальной жидкости при той же температуре. Вся совокупность пор адсорбентов разделяется на три класса: микропоры (r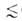 0,6 нм), мезопоры (0,6 нм
0,6 нм), мезопоры (0,6 нм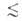 r
r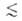 20 нм) и макропоры (r
20 нм) и макропоры (r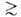 20 нм). А. в микропорах происходит по схеме ТОЗМ, т. е. объемно, в мезопорах-по механизму послойного заполнения, завершаемого капиллярной конденсацией. Макропоры при адсорбц. равновесии никакой роли не играют.
20 нм). А. в микропорах происходит по схеме ТОЗМ, т. е. объемно, в мезопорах-по механизму послойного заполнения, завершаемого капиллярной конденсацией. Макропоры при адсорбц. равновесии никакой роли не играют.
Введя представление о функции распределения объемов пор по значениям хим. потенциала адсорбата в них, М.М. Дубинин и Л. В. Радушкевич получили уравнение изотермы адсорбции ТОЗМ, которое обычно записывают в след. форме:
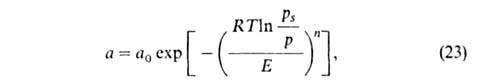
где п, Е и а0-параметры (а0 = а при р = ps). Температурная зависимость a0:
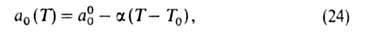
где α= -(da0/dT); a00 = a0 при Т= Т0. Параметры n и Е практически не зависят от температуры. В большинстве случаев n = 2. Лишь для случаев, когда начальные теплоты А. очень велики, 2>п > 2. Для пересчета изотерм А. с одного адсорбтива на другой приближенно допускают, что E1/E2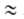 P1/P=
P1/P=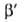 и что a01/a02
и что a01/a02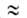 V1/V2,где Pi-парахор, Vi- мольный объем адсорбтива.
V1/V2,где Pi-парахор, Vi- мольный объем адсорбтива.
Каждый микропористый адсорбент характеризуется по ТОЗМ двумя параметрами: W-объемом микропор (W0 = = a0V0) и E0-характеристич. энергией; W0 и E0 относят к стандартному адсорбтиву, обычно к бензолу.
Пользуясь представлением, что в реальном адсорбенте имеются поры разных размеров, и вводя распределение значений Е с дисперсией, равной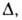 Ф. Стекли предложил обобщение уравнения (23), названное уравнением Дубинина — Стёкли:
Ф. Стекли предложил обобщение уравнения (23), названное уравнением Дубинина — Стёкли:
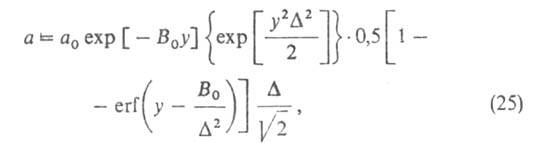
где B0 — константа, связанная с E в уравнении (23), а у=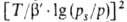 . T.к. в адсорбц. технике наиб. распространение получили именно микропористые адсорбенты (активные угли, цеолиты, тонкопористые ксерогели), ТОЗМ применяется не только в физ.-хим. исследованиях, но и в инженерных расчетах.
. T.к. в адсорбц. технике наиб. распространение получили именно микропористые адсорбенты (активные угли, цеолиты, тонкопористые ксерогели), ТОЗМ применяется не только в физ.-хим. исследованиях, но и в инженерных расчетах.
Адсорбция газовых и жидких смесей. Па практике всегда имеют дело не с индивидуальным адсорбтивом, а со смесью газов или с жидкими растворами. Поэтому требуется обобщение теории А. на случай многокомпонентного адсорбтива. В принципе можно исходить из любой модели А. и распространить ее на этот случай. При А. газовой смеси это достигается не только большим усложнением уравнений, но и введением в них дополнит. эмпирич. параметров, связанных или с взаимод. разнородных молекул или, в более общем виде, с влиянием одних веществ на коэф. активности других. Только модель Ленгмюра позволяет получить уравнение изотермы А. смеси без параметров, не входящих в уравнения для А. индивидуальных веществ. Для этого достаточно учесть, что при адсорбции k-того компонента из смеси i компонентов часть адсорбц. центров м. б. занята др. молекулами. Поэтому:
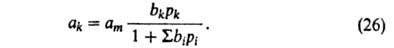
В случае А. жидких растворов независимо от их концентрации вся поверхность адсорбента заполнена. Вследствие этого А. молекулы k-того компонента сопровождается вытеснением не-которого числа молекул остальных компонентов, т. е. А. носит конкурентный характер.
Различают молекулярную и ионную А. растворов. Первая происходит при А. растворов неэлектролитов, вторая-растворов электролитов. Молекулярная А., как правило, выражается избыточными величинами. Конкурентный характер А. обусловливает то, что величина а м. б. как положительной, так и отрицательной. Выражая А. i-того компонента как функцию его мольной доли в растворе хi-, имеем, что Гi = О при хi = 0 и хi = 1 (возможным изменением объема вещества в адсорбц. слое пренебрегают). Поэтому изотерма А. имеет один или неск. экстремумов.
Уравнение изотермы А. бинарных растворов неэлектролитов, надежно обоснованное термодинамически, имеет вид:
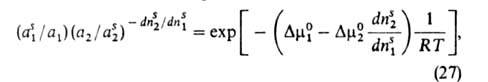
где индекс s указывает на адсорбц. фазу, — (dns2/dns1) показывает, сколько молей второго компонента вытесняется одним молем первого, 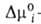 -разность слагаемых (стандартных частей) хим. потенциала, зависящих только от температуры.
-разность слагаемых (стандартных частей) хим. потенциала, зависящих только от температуры.
Осн. проблема использования этого и ряда др. уравнений изотермы А. — выяснение зависимости коэф. активности компонентов в адсорбц. слое от его состава. Важнейший вопрос при применении А. для разделения или очистки веществ-подбор селективного адсорбента по отношению к данному компоненту раствора.
Ионная А., как правило, не носит эквивалентного характера. На поверхности из раствора электролита адсорбируются преим. катионы или анионы. Благодаря электрич. (кулонов-ским) силам на поверхности образуется двойной электрический слой.
Если в состав адсорбента входят ионы или поверхностные функц. группы, способные в данном растворителе к ионизации, то между адсорбентом и раствором электролита происходит ионный обмен. Адсорбент в этом случае наз. ионитом.
Кинетика адсорбции
А., как и любой реальный процесс, происходит во времени. Поэтому полная теория А. должна содержать раздел о кинетике А. Элементарный акт А. осуществляется практически мгновенно (исключение-хемосорбция). Поэтому временные зависимости А. определяются в осн. механизмом диффузии, т. е. подвода адсорбтива к месту А. Если А. на открытой поверхности не мгновенна, такой процесс происходит во внешнедиффузионной области; при этом законы диффузии не специфичны для А. В случае же пористых адсорбентов, кроме внеш. диффузии, важную роль начинает играть внутр. диффузия, т. е. перенос адсорбтива в порах адсорбента при наличии в них градиента концентрации. Механизм такого переноса может зависеть от концентрации адсорбтива и размеров пор.
Различают молекулярную, кнудсеновскую и поверхностную (фольмеровскую) диффузию. Молекулярная диффузия осуществляется, если длина своб. пробега молекул в порах меньше размера пор, кнудсеновская-если эта длина превышает размер пор. При поверхностной диффузии молекулы перемещаются по поверхности адсорбента без перехода в объемную фазу. Однако значения коэф. диффузии не одинаковы для разных механизмов диффузии. Во мн. случаях экспериментально не удается установить, как именно происходит диффузия, и поэтому вводят т. наз. эффективный коэф. диффузии, описывающий процесс в целом.
Осн. эксперим. материалом о кинетике А. служит т. наз. кинетич. кривая, т. е. функция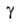 = а/аравн=f(t) где
= а/аравн=f(t) где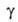 -относительная А., равная отношению текущего значения адсорбции а к aравн — её значению при времени t
-относительная А., равная отношению текущего значения адсорбции а к aравн — её значению при времени t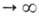 . Для истолкования кинетич. кривой в простейшем случае предполагают, что зерно адсорбента имеет совершенно однородную по объему пористую структуру (эту модель наз. квазигомогенной). значит. усовершенствование квазигомогенной модели-представление о том, что каждое зерно содержит области с более крупными и более тонкими порами. Диффузия в таком зерне описывается двумя разл. коэффициентами.
. Для истолкования кинетич. кривой в простейшем случае предполагают, что зерно адсорбента имеет совершенно однородную по объему пористую структуру (эту модель наз. квазигомогенной). значит. усовершенствование квазигомогенной модели-представление о том, что каждое зерно содержит области с более крупными и более тонкими порами. Диффузия в таком зерне описывается двумя разл. коэффициентами.
В случае открытой поверхности, принимая модель Ленгмюра, легко получить кинетич. уравнение А. Скорость приближения к равновесию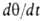 представляет собой разность скоростей А. и десорбции. Считая, как обычно в кинетике, что скорости процессов пропорциональны концентрациям реагирующих веществ, имеем:
представляет собой разность скоростей А. и десорбции. Считая, как обычно в кинетике, что скорости процессов пропорциональны концентрациям реагирующих веществ, имеем:
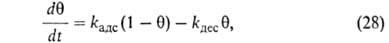
где kадс и kдес- константы скорости соотв. А. и десорбции. Давление в газовой фазе считается постоянным. При интегрировании этого уравнения от t = 0 до любого значения t получим:
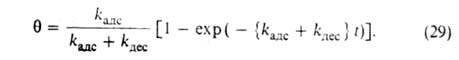
Отсюда при f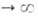 имеем:
имеем: 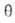 =
=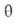 равн. Поэтому окончательно имеем:
равн. Поэтому окончательно имеем:
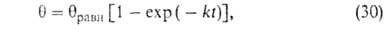
где k = kадс + kдес.
Влияние температуры на скорость А. выражается уравнением, аналогичным уравнению Аррениуса. С увеличением температуры kадс экспоненциально возрастает. Т.к. диффузия в порах адсорбента связана с преодолением активац. барьеров, температурные зависимости kадс и kдес не одинаковы.
Знание скоростей диффузии важно не только для теории А., но и для расчета пром. адсорбц. процессов. При этом обычно имеют дело не с отдельными зернами адсорбента, а с их слоями. Кинетика процесса в слое выражается очень сложными зависимостями. В каждой точке слоя в данный момент времени величина А. определяется не только видом уравнения изотермы А. и закономерностями кинетики процесса, но также аэро- или гидродинамич. условиями обтекания зерен газовым или жидкостным потоком. Кинетика процесса в слое адсорбента в отличие от кинетики в отдельном зерне наз. динамикой А., общая схема решения задач которой такова: составляется система дифференц. уравнений в частных производных, учитывающая характеристики слоя, изотерму А., диффузионные характеристики (коэф. диффузии, виды переноса массы по слою и внутри зерен), аэро- и гидродинамич. особенности потока. Задаются начальные и краевые условия. Решение этой системы уравнений в принципе приводит к значениям величин А. в данный момент времени в данной точке слоя. Как правило, аналитич. решение удается получить только для простейших случаев, поэтому такая задача решается численно с помощью ЭВМ.
При опытном изучении динамики А. через слой адсорбента пропускают газовый или жидкостный поток с заданными характеристиками и исследуют состав выходящего потока как функцию времени. Появление поглощаемого вещества за слоем наз. проскоком, а время до проскока — временем защитного действия. Зависимость концентрации данного компонента за слоем от времени наз. выходной кривой. Эти кривые служат осн. эксперим. материалом, позволяющим судить о закономерностях динамики А.
Аппаратурное оформление адсорбционных процессов
Существует множество технол. приемов проведения адсорбц. процессов. Широко распространены циклич. (перио-дич.) установки с неподвижным слоем адсорбента, осн. узел которых — один или неск. адсорберов, выполненных в виде полых колонн, заполняемых гранулированным адсорбентом. Газовый (или жидкостной) поток, содержащий адсорбируемые компоненты, пропускается через слой адсорбента до проскока. После этого адсорбент в адсорбере регенерируют, а газовый поток направляют в др. адсорбер. Регенерация адсорбента включает ряд стадий, из которых ос новная-десорбция, т. е. выделение ранее поглощенного вещества из адсорбента. Десорбцию проводят нагреванием, сбросом давления в газовой фазе, вытеснением (напр., острым водяным паром) или комбинацией этих методов. Т. к. времена А. и регенерации не совпадают, подбирают такое число одновременно работающих и регенерируемых адсорберов, чтобы в целом процесс шел непрерывно.
По техн. и экономич. соображениям регенерацию не доводят до конца. Поэтому рабочая емкость адсорбента равна разности между максимально достигаемой в данных условиях А. и количеством адсорбата, остающегося в адсорбенте после регенерации. Вследствие этого изотермы А., соответствующие процессу в адсорбере, не должны быть слишком крутыми.
В описанной схеме возможны два варианта: 1) целевой продукт адсорбируется из газового потока практически полностью, и тогда он содержится в десорбате, откуда его извлекают тем или иным способом; 2) целевой продукт адсорбируется хуже, чем др. компоненты газовой смеси, и тогда он содержится в выходящем газовом потоке. По первому варианту работают, напр., рекуперационные установки на вискозных производствах, улавливающие из отходящих газов и возвращающие в цикл CS2. Производительность таких установок достигает сотен тысяч м3 очищаемого газа в час; адсорбент-активный уголь с не слишком тонкими микропорами, т. е. уголь, в котором константа E по ТОЗМ (см. выше) равна 20–25 кДж/моль. Это значение E0 соответствует не слишком крутой изотерме, что обеспечивает хорошие условия регенерации. Такие угли наз. рекуперационными. Десорбцию осуществляют острым водяным паром. Для экономии энергии холодные и газовые горячие потоки пропускают через теплообменники.
Очень важна осушка газов и жидкостей, напр. нефтяных газов перед их переработкой или прир. газов перед транспортировкой; адсорбенты-силикагель или цеолиты. Десорбцию осуществляют нагреванием. Т. к. десорбция цеолита связана с большими энергозатратами, применяют комбинированный адсорбент: осн. массу влаги поглощают легко регенерируемым силикагелем, а глубокую доосушку-цеолитом.
При тепловой регенерации полный цикл включает А., нагрев адсорбента, его десорбцию и охлаждение. Большое число стадий обусловливает низкую интенсивность и высокую энергоемкость процесса. Поэтому широкое распространение получили т. наз. короткоцикловые установки, весь цикл в которых занимает неск. минут. В них газ подается в адсорбер под значит. давлением, которое затем сбрасывается, и происходит десорбция. Весь процесс идет почти изотермически (отклонение от изотермичности вызывается только выделением теплоты А. и поглощением теплоты при десорбции). Стадии цикла: А., сброс давления, десорбция, подъем давления. Пример-установки с цеолитом для получения воздуха, обогащенного кислородом.
В установках сдвижущимся слоем адсорбента (в т. наз. гиперсорберах) последний под действием силы тяжести медленно опускается, выводится из ниж. части адсорбера и попадает в т. наз. эрлифт, представляющий собой вертикальную трубу, параллельную адсорбц. колонне. По этой трубе снизу вверх движется поток воздуха, который поднимает зерна адсорбента в верх. часть колонны. Перерабатываемый газовый поток поступает в среднюю часть адсорбера и движется вверх противотоком к адсорбенту. В верхней части колонны непрерывно происходит А., в нижней — регенерация адсорбента (см. также адсорбционная очистка).
В установках с псевдоожиженным ("кипящим") слоем адсорбента газовый поток, поступающий в адсорбер снизу, приводит адсорбент во взвешенное состояние. При этом резко увеличивается эффективность массообмена между адсорбентом и газом и сокращается длительность А. и десорбции. Такие установки имеют высокую производительность. Их широкому распространению препятствуют высокие требования, предъявляемые к мех. прочности зерен адсорбента (недостаточная прочность обусловливает значит. потери адсорбента вследствие его истирания и уноса из аппарата).
Осн. требования к адсорбентам: большая адсорбц. емкость, т. е. они должны представлять собой дисперсные тела с большой уд. поверхностью или с большим объемом пор; хим. природа поверхности должна обеспечивать эффективную А. данных веществ в данных условиях; хим. и термич. стойкость, регенерируемость, доступность. Наиб. распространение получили активные угли, ксерогели некоторых оксидов (силика-гели, алюмогели и др.), цеолиты; из непористых адсорбентов-техн. углерод (сажа) и высокодисперсный SiO2 (аэросил, "белая сажа").
Области применения адсорбционной техники
На явлении А. основаны мн. способы очистки воздуха от вредных примесей (см. газов очистка), воды (см. водоподготовка), а также сахарных сиропов при сахароварении, фруктовых соков и др. жидкостей в пищ. промышленности, отработанных смазочных масел. Удаление влаги как вредной примеси из газов и жидкостей с помощью твердых адсорбентов-одна из важных отраслей адсорбц. техники (см. также газов осушка).
На адсорбц. процессах основано тонкое разделение смесей веществ и выделение из сложных смесей определенных компонентов. Примеры-разделение изомеров алканов с целью получения нормальных углеводородов для производства ПАВ, разделение нефтей при производстве моторных топлив. Для газовых смесей адсорбц. методы разделения используют при получении воздуха, обогащенного кислородом (вплоть до почти чистого O2); во мн. случаях эти методы успешно конкурируют с ректификационным (см. воздуха разделение).
Быстро развивающаяся область применения адсорбц. техники-медицина, где она служит для извлечения вредных веществ из крови (метод гемосорбции) и др. физиол. жидкостей. Высокие требования к стерильности ставят очень трудную задачу подбора подходящих адсорбентов. К ним относятся специально приготовленные активные угли.
Лит.: Брунауэр С., Адсорбция газов и паров, пер. с англ., т. 1, М., 1948; де Бур Я, Динамический характер адсорбции, пер. с англ., М., 1962; Адсорбция и пористость, под ред. М. М. Дубинина [и др.], М., 1976; Кельиев Н. В., Основы адсорбционной техники, 2 изд., М., 1984; Young D.M., Crowell A.D., Physical adsorption of gases, L., 1962.
М. М. Дубинин, В. В. Серпинский
Значения в других словарях
- АДСОРБЦИЯ — (от лат. ad — на, при и sorbeo — поглощаю), процесс, приводящий к аномально высокой концентрации в-ва (а д с о р б а т а) из газообразной или жидкой среды на поверхности её раздела с жидкостью или тв. телом (а д с о р б е н т о м). Частный случай сорбции. Физический энциклопедический словарь
- адсорбция — Поглощение вещества из раствора или газа поверхностным слоем жидкости или твердого тела (адсорбентом); играет важную роль в биол. системах, широко применяется в биохимии для разделения и очистки веществ. Микробиология. Словарь терминов
- адсорбция — -и, ж. физ., хим. Поглощение частиц газа или растворенного вещества поверхностным слоем жидкого или твердого вещества. [От лат. ad — к и sorbere — поглощать, всасывать] Малый академический словарь
- Адсорбция — Поглощение вещества из газа или раствора поверхностью раздела между ними (или поверхностью твердого тела). Иными словами, А. есть поглощение адсорбата из объема фаз на поверхности адсорбента. А. является частным случаем сорбции. Математическая энциклопедия
- адсорбция — Адсорбция — концентрирование вещества на поверхности раздела двух фаз, происходящее под влиянием молекулярных сил поверхности адсорбента. В результате А. свободная поверхностная энергия уменьшается. Толковый словарь по почвоведению
- Адсорбция — (от лат. ad — на, при и sorbeo — поглощаю) поглощение к.-л. вещества из газообразной среды или раствора поверхностным слоем жидкости или твёрдого тела. Например, если поместить в водный раствор уксусной кислоты кусочек угля, то произойдёт... Большая советская энциклопедия
- адсорбция — АДСОРБЦИЯ и, ж. adsorption f. <�лат. ad при + sorbere поглощать, всасывать. спец. Поглощение, всасывание вещества из раствора или газа поверхностью твердого тела или поверхностным слоем жидкости. Явления адсорбции. Адсорбция газов. Словарь галлицизмов русского языка
- Адсорбция — (лат. adsorbeo — поглощаю) поглощение газов, паров и жидкостей поверхностным слоем твердого тела (адсорбента) или жидкости. Используется для забора запаховых следов с места происшествия; лежит в основе многих методов хроматографии. Криминалистическая энциклопедия
- адсорбция — АДСОРБЦИЯ — концентрирование вещества на поверхности раздела двух фаз, происходящее под влиянием молекулярных сил поверхности адсорбента. Ботаника. Словарь терминов
- адсорбция — Ад/со́рб/ци/я [й/а]. Морфемно-орфографический словарь
- адсорбция — орф. адсорбция, -и Орфографический словарь Лопатина
- АДСОРБЦИЯ — АДСОРБЦИЯ, притяжение газа или жидкости к поверхности твердого тела или жидкости, в отличие от абсорбции, при которой подразумевается проникновение одного вещества в другое (как, например, губка пропитывается водой). Научно-технический словарь
- Адсорбция — (от лат. ad — y, на, при и sorbeo — поглощаю * a. adsorption; н. Adsorption, Adsorbieren, Adsorbierung; ф. adsorption; и. adsorcion) — поглощение отд. Горная энциклопедия
- Адсорбция — (Ад- + лат. sorbeo поглощать) поглощение (концентрирование) газов или растворенных веществ на поверхности твердого тела или жидкости. Медицинская энциклопедия
- адсорбция — АДСОРБЦИЯ -и; ж. [от лат. ad- — к и sorbere — поглощать, всасывать]. Поглощение вещества из газа или раствора поверхностным слоем жидкого или твёрдого адсорбента (используется в химии, технике и т.п. для разделения и очистки веществ). ◁ Адсорбционный, -ая, -ое. Толковый словарь Кузнецова
- адсорбция — адсорбция ж. Поглощение, всасывание вещества из раствора или газа поверхностью твёрдого тела или поверхностным слоем жидкости. Толковый словарь Ефремовой
- адсорбция — [лат. ad при, к + sorbere глотать] – поверхностное поглощение; поглощение какого-либо вещества из газообразной среды или раствора поверхностным слоем другого вещества в отличие от абсорбции – поглощения всем объёмом вещества Большой словарь иностранных слов
- АДСОРБЦИЯ — АДСОРБЦИЯ (от лат. ad — на, при и sorbeo — поглощаю) — поглощение газов, паров или жидкостей поверхностным слоем твердого тела (адсорбента) или жидкости. Адсорбенты обычно имеют большую удельную поверхность — до нескольких сотен м2/г. Большой энциклопедический словарь
