Магнитный момент

Магни́тный момент

Основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток. Из опыта и классической теории электромагнитного поля следует, что магнитные действия замкнутого тока (контура с током) определены, если известно произведение (М) силы тока i на площадь контура σ (М = i σ/c в СГС системе единиц (См. СГС система единиц), с — скорость света). Вектор М и есть, по определению, М. м. Его можно записать и в иной форме: М = m l, где m — эквивалентный Магнитный заряд контура, а l — расстояние между «зарядами» противоположных знаков (+ и -).

М. м. обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. М. м. элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — Спина. М. м. ядер складываются из собственных (спиновых) М. м. образующих эти ядра протонов и нейтронов, а также М. м., связанных с их орбитальным движением внутри ядра. М. м. электронных оболочек атомов и молекул складываются из спиновых и орбитальных М. м. электронов. Спиновый магнитный момент электрона m_сп может иметь две равные и противоположно направленные проекции на направление внешнего магнитного поля Н. Абсолютная величина проекции

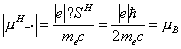
где μ_в= (9,274096 ±0,000065)·10^-21эрг/гс — Бора магнетон, 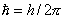, где h — Планка постоянная, е и m_e — заряд и масса электрона, с — скорость света; S^H — проекция спинового механического момента на направление поля H. Абсолютная величина спинового М. м.

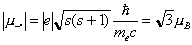
где s = ¹/₂ — спиновое квантовое число (См. Квантовые числа). Отношение спинового М. м. к механическому моменту (спину)

,

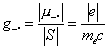так как спин

.

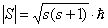Исследования атомных спектров показали, что m^Н_сп фактически равно не m_в, а m_в (1 + 0,0116). Это обусловлено действием на электрон так называемых нулевых колебаний электромагнитного поля (см. Квантовая электродинамика, Радиационные поправки).

Орбитальный М. м. электрона m_орб связан с механическим орбитальным моментом 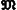_орб соотношением g_opб = |m_орб| / |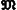_орб| = |e|/2m_ec, то есть Магнитомеханическое отношение g_opб в два раза меньше, чем g_cп. Квантовая механика допускает лишь дискретный ряд возможных проекций m_орб на направление внешнего поля (так называемое Квантование пространственное): m^Н_орб = m_lm_в, где m_l — магнитное квантовое число, принимающее 2l + 1 значений (0, ±1, ±2,..., ±l, где l — орбитальное квантовое число). В многоэлектронных атомах орбитальный и спиновый М. м. определяются квантовыми числами L и S суммарного орбитального и спинового моментов. Сложение этих моментов проводится по правилам пространственного квантования. В силу неравенства магнитомеханических отношений для спина электрона и его орбитального движения (g_cп ¹ g_opб) результирующий М. м. оболочки атома не будет параллелен или антипараллелен её результирующему механическому моменту J. Поэтому часто рассматривают слагающую полного М. м. на направление вектора J, равную

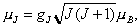
где g_J — магнитомеханическое отношение электронной оболочки, J — полное угловое квантовое число.

М. м. протона, спин которого равен

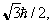
должен был бы по аналогии с электроном равняться

,

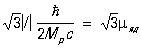где M_p — масса протона, которая в 1836,5 раз больше m_e, m_яд — ядерный магнетон, равный 1/1836,5m_в. У нейтрона же М. м. должен был бы отсутствовать, поскольку он лишён заряда. Однако опыт показал, что М. м. протона m_p = 2,7927m_яд, а нейтрона m_n = —1,91315m_яд. Это обусловлено наличием мезонных полей около нуклонов, определяющих их специфические ядерные взаимодействия (см. Ядерные силы, Мезоны) и влияющих на их электромагнитные свойства. Суммарные М. м. сложных атомных ядер не являются кратными m_яд или m_p и m_n. Таким образом, М. м. ядра калия 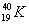равен —1,29 m_яд. Причиной этой неаддитивности является влияние ядерных сил, действующих между образующими ядро нуклонами. М. м. атома в целом равен векторной сумме М. м. электронной оболочки и атомного ядра.

Для характеристики магнитного состояния макроскопических тел вычисляется среднее значение результирующего М. м. всех образующих тело микрочастиц. Отнесённый к единице объёма тела М. м. называется намагниченностью. Для макротел, особенно в случае тел с атомным магнитным упорядочением (ферро-, ферри- и антиферромагнетики), вводят понятие средних атомных М. м. как среднего значения М. м., приходящегося на один атом (ион) — носитель М. м. в теле. В веществах с магнитным порядком эти средние атомные М. м. получаются как частное от деления самопроизвольной намагниченности ферромагнитных тел или магнитных подрешёток в ферри- и антиферромагнетиках (при абсолютном нуле температуры) на число атомов — носителей М. м. в единице объёма. Обычно эти средние атомные М. м. отличаются от М. м. изолированных атомов; их значения в магнетонах Бора m_в оказываются дробными (например, в переходных d-металлах Fe, Со и Ni соответственно 2,218 m_в, 1,715 m_в и 0,604 m_в) Это различие обусловлено изменением движения d-электронов (носителей М. м.) в кристалле по сравнению с движением в изолированных атомах. В случае редкоземельных металлов (лантанидов), а также неметаллических ферро- или ферримагнитных соединений (например, ферриты) недостроенные d- или f-слои электронной оболочки (основные атомные носители М. м.) соседних ионов в кристалле перекрываются слабо, поэтому заметной коллективизации этих слоев (как в d-металлах) нет и М. м. таких тел изменяются мало по сравнению с изолированными атомами. Непосредственное опытное определение М. м. на атомах в кристалле стало возможным в результате применения методов магнитной нейтронографии, радиоспектроскопии (ЯМР, ЭПР, ФМР и т.п.) и Мёссбауэра эффекта. Для парамагнетиков также можно ввести понятие среднего атомного М. м., который определяется через найденную на опыте постоянную Кюри, входящую в выражение для Кюри закона или Кюри — Вейса закона (см. Парамагнетизм).

Лит.: Тамм И. Е., Основы теории электричества, 8 изд., М., 1966; Ландау Л. Д. и Лифшиц Е. М., Электродинамика сплошных сред, М., 1959; Дорфман Я. Г., Магнитные свойства и строение вещества, М., 1955; Вонсовский С. В., Магнетизм микрочастиц, М., 1973.

С. В. Вонсовский.