Изоморфизм

I

Изоморфи́зм (от Изо... и греч. morphé — вид, форма)

свойство веществ, аналогичных по химическому составу, кристаллизоваться в одинаковых формах. Впервые было показано немецким минералогом Э. Мичерлихом (1819) на примере KH₂PO₄, KH₂AsO₄ и NH₄H₂PO₄. Вскоре было обнаружено, что первые два вещества образуют смешанные кристаллы («твёрдые растворы») с единой внешней формой при произвольном отношении P : As, в то время как в других парах аналогичные замещения ограничены количественно. Первый случай отвечает понятию «совершенный И.», а второй — понятию «ограниченный», или «несовершенный И.». Если количества замещающего элемента невелики, но существенны для поисковика минералога-геохимика, то говорят об эндокриптии (по А. Е. Ферсману, замещение узлов кристаллических решёток ионами того же знака, но разных свойств и мало сходных величин). Требование родственности взаимозамещающихся элементов при И. первоначально понималось как чисто химическая близость, и первые ряды изоморфных элементов (В. И. Вернадский; см. Геохимия) повторяли группы менделеевской системы с некоторыми дополнениями известных из аналитической химии групп, например Al, Cr, Fe. Выяснилось, однако, что невозможно, например, замещение Na на Rb; твёрдые растворы К- и Na-coeдинений энергично распадаются при низких температурах (распад К-, Na-полевых шпатов). Решающим для объяснения этих явлений при И. было введение (В. М. Гольдшмидт, 1926) представления об ионных радиусах (См. Ионные радиусы), близость которых стала одним из основных условий И. У полновалентных катионов (Na¹⁺, Mg²⁺,..., S⁶⁺,...) ионный радиус r быстро уменьшается вдоль строки менделеевской системы и резко увеличивается вдоль вертикали на величины, большие чем 10—15% (экспериментальный предел для возможности И.). В результате изоморфными оказываются элементы, соседние по диагоналям (Д. И. Менделеев, А. Е. Ферсман), например ряд Na—Ca (r_Na = 0,98Å, r_Ca = 1,02Å), который представлен в плагиоклазах, составляющих более 50% земной коры. Эта диагональ продолжается к редкоземельным элементам, и именно благодаря постоянному изоморфному вхождению редкоземельных элементов в Са-минералы эти элементы долгое время считались двухвалентными (только Д. И. Менделеев перевёл их в III группу). Другие характерные «диагональные» пары: Li—Mg, Mo—Re, Be—Al и т. д. Если, однако, строки менделеевской системы длинные (с 32 клетками), то описанное сокращение радиусов вдоль строки заходит так далеко, что катионы одной и той же менделеевской группы выравнивают свои радиусы, т. е. у элементов одной группы, разделённых по вертикали «лантанидным сжатием», И. становится весьма ярко выраженным. Это относится к парам Ba—Ra, Zr—Hf, Nb—Ta и др. Но как ни близки между собой Nb и Ta, их легче отделить друг от друга, чем отделить от Ti, с которым они связаны диагональным изоморфизмом. Таким образом, изовалентный И. представлен намного скромнее (во всяком случае количественно), чем гетеровалентный И. Возникает вопрос, как компенсировать в структуре кристалла изменение валентности, например её увеличение при И. Ca²⁺ → Na¹⁺. Решение просто, когда элемент на середине диагонали замещается двумя соседними по разные стороны, например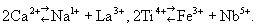

Особенно часто компенсация достигается за счёт одновременного гетеровалентного И. «в обратном направлении». В плагиоклазах замена Ca²⁺ на Na¹⁺ сопровождается параллельно замещением Al³⁺ на Si⁴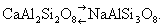⁺: Возникает вопрос, как быть с радиусами Si⁴⁺(0,39Å) и Al³⁺(0,57Å), различающимися на 46%. Значительная разница между радиусами не является препятствием при гетеровалентном И., так как в анионной, более отрицательной части соединений заменяют друг друга не атомы, а тетраэдрические группы, например SiO^4-₄ и AlO^5-₄, в которых эффективные расстояния Si—О и Al—О (1,72 и 1,90 ) разнятся всего лишь на 9%. Литий, например, в более «катионной» форме, имеющий координацию 6, замещает по правилу диагонали Mg (в биотитах); находясь же среди четырёх О, способен заменить Be в берилле: [LiO₄] → [BeO₄]. Разобранные закономерности касаются в основном случаев изоморфных замещений между полновалентными ионами типа «благородных газов» в соединениях, которые подчиняются законам элементарной энергетики (формулы А. Ф. Капустинского). Для переходных металлов, образующих соединения существенно ковалентного типа и стремящихся создать возле себя за счёт донорско-акцепторного механизма группы электронов 8, 13—14, 18, закономерности И. иные. Так, в случае пары элементов с одним и тем же радиусом, например Zn²⁺ и Fe²⁺, мы встречаемся с односторонним И. Цинк в своём главном соединении ZnS (сфалерит) допускает вхождение до 20% Fe, но Zn совершенно отсутствует в FeS. Причина лежит в возможности для Fe иметь как шестерную координацию, так и четверную, тогда как для Zn всегда в сульфидах — четверная координация.

И. очень распространён в природе. Широким развитием изоморфных замещений объясняется сложный химический состав большинства минералов, особенно из группы силикатов (См. Силикаты). Примером совершенного И. являются минералы переменного состава, дающие непрерывные ряды: плагиоклазы, скаполиты, вольфрамиты и др. Законы изоморфного замещения объясняют распределение редких элементов, находящихся в виде примесей в горных породах и рудах. Так, значительная часть иттрия и редких земель находится в апатите, сфене и флюорите, изоморфно замещая кальций; трёхвалентный ванадий замещает в магнетите окисное железо; селен — серу в пирите и т. д. Учение об И. является основой для изучения форм нахождения элементов в горных породах и процессов концентрации и рассеяния химических элементов в земной коре.

Лит.: Вернадский В. И., Очерки геохимии, 4 изд., М. — Л., 1934; Ферсман А. Е., Геохимия, 2 изд., т. 1, Л, 1934; Менделеев Д. И., Соч., т. 1, Л., 1937; Гольдшмидт В. М., Кристаллохимия, пер. с нем., Л., 1937; Сто лет периодического закона химических элементов, М., 1969.

Н. В. Белов.

II

Изоморфи́зм

одно из основных понятий современной математики, возникшее сначала в пределах алгебры в применении к таким алгебраическим образованиям, как группы (См. Группа), кольца (См. Кольцо), поля (См. Поле) и т. п., но оказавшееся весьма существенным для общего понимания строения и области возможных применений каждого раздела математики.

Понятие И. относится к системам объектов с заданными в них операциями или отношениями. В качестве простого примера двух изоморфных систем можно рассмотреть систему R всех действительных чисел с заданной на ней операцией сложения x = x₁+ x₁ и систему Р положительных действительных чисел с заданной на ней операцией умножения y = y₁y₂. Можно показать, что внутреннее «устройство» этих двух систем чисел совершенно одинаково. Для этого достаточно систему R отобразить в систему Р, поставив в соответствие числу х из R число у = a^x (а > 1) из Р. Тогда сумме x = x₁ + x₂ будет соответствовать произведение y = y₁y₂ чисел 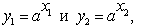соответствующих x₁ и x₂. Обратное отображение Р на R имеет при этом вид x = log_a y. Из любого предложения, относящегося к сложению чисел системы R, можно извлечь соответствующее ему предложение, относящееся к умножению чисел системы Р. Например, если в R сумма

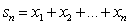
членов арифметической прогрессии выражается формулой

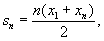
то в Р произведение

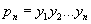
членов геометрической прогрессии выражается формулой

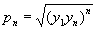
(умножению на n в системе R соответствует при переходе к системе Р возведение в n-ю степень, а делению на два — извлечение квадратного корня).

Изучение свойств одной из изоморфных систем в значительной мере (а с абстрактно-математической точки зрения — полностью) сводится к изучению свойств другой. Любую систему объектов S', изоморфную системе S, можно рассматривать как «модель» системы S («моделировать систему S при помощи системы S' ») и сводить изучение самых разнообразных свойств системы S к изучению свойств «модели» S'.

Общее определение И. систем объектов с заданными на них в конечном числе отношениями между постоянным для каждого отношения числом объектов таково. Пусть даны две системы объектов S и S', причём в первой определены отношения

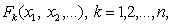
а во второй — отношения

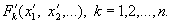
Системы S и S' с указанными в них отношениями называются изоморфными, если их можно поставить в такое взаимно однозначное соответствие

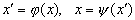
(где х — произвольный элемент S, а x' — произвольный элемент S'), что из наличия F_k (x₁,x₂,...) вытекает F'_k (х'₁,х'₂,...), и наоборот. Само указанное соответствие называется при этом изоморфным отображением, или изоморфизмом. [В приведённом выше примере в системе R определено отношение F (x, x₁, x₂), где x = x₁ + x₂, в системе Р — отношение F' (y, y₁, y₂), где у = у₁у₂; взаимно однозначное соответствие устанавливается по формулам у = a^x, х = 1og_ay.]

Понятие И. возникло в теории групп, где впервые был понят тот факт, что изучение внутренней структуры двух изоморфных систем объектов представляет собой одну и ту же задачу.

Аксиомы любой математической теории определяют систему объектов, изучаемую этой теорией, всегда только с точностью до И.: аксиоматически построенная математическая теория, применимая к какой-либо одной системе объектов, всегда полностью применима и к другой. Поэтому каждая аксиоматически изложенная математическая теория допускает не одну, а много «интерпретаций», или «моделей» (см., например, в ст. Геометрия, раздел Истолкование геометрии).

Понятие И. включает в себя как частный случай понятие Гомеоморфизма, играющее основную роль в топологии (См. Топология).

Частным случаем И. является автоморфизм — взаимно однозначное отображение

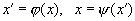
системы объектов с заданными отношениями F_k(x₁, x₂, ...) на самоё себя, при котором из F_k(x₁, x₂, ...) вытекает F'_k(x'₁, x'₂, ...), и наоборот. Это понятие тоже возникло в теории групп, но потом оказалось существенным в самых различных разделах математики.

Лит.: Курош А. Г., Курс высшей алгебры, 3 изд., М. — Л., 1952; Энциклопедия элементарной математики, под ред. П. С. Александрова [и др.], кн. 2, М. — Л., 1951.