Тригонометрия

Соотношения между сторонами и углами треугольников (см.) выражаются при помощи особого рода функций, назыв. тригонометрическими. Этим функциям даны особые названия: синус, косинус, тангенс, котангенс, секанс и косеканс.

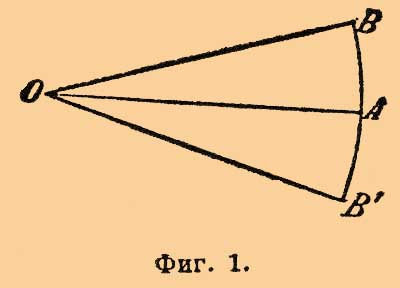
Фиг 1.

Предположим, что, приняв точку О за центр, радиусом ОА опишем дугу AB. Точка А наз. началом дуги AB, а точка В — концом дуги AB. Представим себе угол АОВ, вершина которого находится в точке О, а стороны проходят через точки А и В. При изменении радиуса ОА дуга AB, ограниченная сторонами данного угла, меняется, но отношение AB/OA остается неизменным. Это отношение служит мерою данного угла. Так как равные углы можно отложить по разные стороны прямой ОА, то, для того, чтобы отличить один угол от другого, согласились один из углов выражать числом положительным, а другой числом отрицательным. Если дуги AB и AB', описанные радиусом ОА равны, то и угол АОВ равен углу АОВ'. Если напр. AB/OA = 1/3, то согласимся говорить, что угол АОВ равен 1/3 и что угол АОВ' равен (— 1/3). Таким образом всякому отвлеченному числу (положительному или отрицательному) соответствует вполне определенный угол. Если мы из конца дуги В опустим перпендикуляры ВР и BQ на прямую ОА и на прямую ОС, перпендикулярную к ОА, то получим отрезки ОР и OQ (черт. 2), которые назыв. проекциями 0В на ОА и на ОС. Предположим, что угол АОВ не меняется, а изменяется радиус ОА; в таком случае отношения ОР/OA и OQ/OA остаются неизменными.

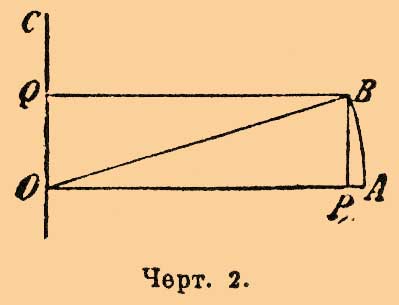
Черт. 2.

Здесь возможны следующие частные случаи. Проекция 0В на О А может быть направлена в ту же сторону, как и отрезок ОА или же в сторону противоположную (черт. 3).

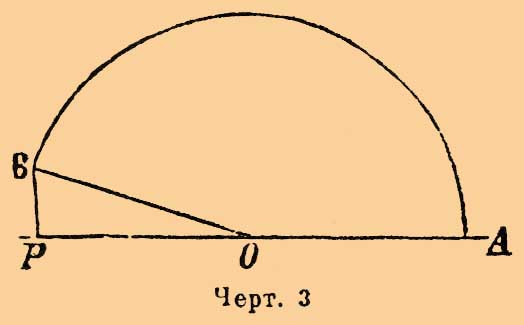
Черт. 3.

Точно так же проекция 0В на ОС может иметь направление ОС или направление противоположное (черт. 4).

Черт. 4.

Направление ОС выбрано так, чтобы прямой

угол А ОС был положительный. Если угол АОВ равен α, то синусом α (Sinα) назыв. отношение OQ/OA в случае, если OQ имеет одинаковое направление с ОС. Если же OQ направлено противоположно ОС, то

Sinα = — OQ/OA

Отношение OP/OA назыв. косинусом α, (Cosα) в случае, если ОР одинаково направлено с OA. Если же ОР имеет противоположное направление с ОА, то

Cosα = — OP/OA

В учебниках Т. можно найти доказательство следующих формул:

Sin (—α) = — Sinα, Cos (—α) = Cosα,

Sin (π/2 — α) = Cosα, Cos (π/2 — α) = Sinα,

Sin (π — α) = Sinα, Cos (π — α) = —Cosα,

Sin (π + α) = — Sinα, Cos (π + a) = —Cosα,

Sin (2π — α) = — Sinα, Cos (2π — α) = Cosα,

Sin (2π + α) = Sinα, Cos (2π + α) —Cosα.

При помощи этих формул вычисление Sinα и Cosα приводится к случаю, когда α число положительное, не превосходящее π/4

Из формул

Sin (α + β) = Sinα Cosß + Cosα Sinß,

Cos (α + ß) = Cosα Cosß — Sinα Sinß

следует

Sina + Sinb = 2Sin[(a + b)/2] Cos[(a — b)/2],

Sina — Sinb = 2Sin[(a — b)/2] Cos[(a + b)/2],

Cosa + Cosb = 2Cos[(a + b)/2] Cos[(a — b)/2],

Cosa — Cosb = 2Sin[(a + b)/2] Sin[(a — b)/2].

Функции Sin2α и Cos2α выражаются через Sinα и Cosα следующим образом:

Sin2α = 2Sinα Cosα,

Cos2α = Cos²α — Sin²α.

Вследствие соотношения

Cos²α + Sin²α = 1

последняя формула принимает следующие виды;

Cos2a = 1 — 2Sin²α или Cos2a = SCos²α — 1.

Здесь для сокращения написано Sin²α и Cos²a вместо (Sinα)² и (Cosα)². Тригонометри-ческие функции тангенс (tg), котангенс (ctg), секанс (sec) и косеканс (cosec) определяются следующим образом:

tgα = Sinα/Cosα, ctgα = Cosα/Sinα,

secα = 1/Cosα, cosecα = 1/Sinα

Отметим некоторые свойства тангенса.

tg(α + β) = (tgα + tgβ)/(1 — tgαtgβ)

tg2α = (2tgα)/(1 — tg²α)

tgα/2 = Sinα/(1 + Cosα) = (1 — Cosα)/Sinα

Функции обратные тригонометрическим наз. круговыми: арксинус (arc Sin), арккосинус (arc Cos), арктангенс (arc tg), арккотангенс (arc ctg), арксеканс (arc sec) и арккосеканс (arc cosec). Если напр. tgα = a, то α = arc tga. Так как данному числу a соответствует множество различных α, то для большей определенности согласились под arc tga понимать число, лежащее в промежутке (— π/2, π/2). В этом промежутке тангенс может иметь любое значение. Подобным же образом предполагается, что числа arc Sina, arc ctga и arc coseca лежат между — π/2 и π/2, а числа arc Cosa и arc seca между О и π. Тригонометрические функции имеют очень важное значение: они встречаются в очень многих вопросах анализа и геометрии. Так как вычисления облегчаются при помощи логарифмов, то в таблицах помещаются не самые тригонометрические функции, но их логарифмы (см.). Углы в таблицах выражены не числами, а градусами. Если данный угол равен α, то он содержит 180α/π градусов; 60-ая часть градуса наз. минутой, а 60-ая часть минуты — секундой. Тригонометрические таблицы вычисляются при помощи рядов (см.).

Соотношения между сторонами и углами прямолинейного треугольника (см.) выражаются следующими формулами. Если обозначим углы треугольника через A, В и С, а противолежащие им стороны через a, b и с, то получим

А + B + С = π,

SinA/a = SmB/b = SinC/c

a² = b² + с² — 2bc.CosA,

a = b.CosC + c.CosB,

tg[(Α — Β)/2] = [(a — b)/(a + b)]Ctg(С/2)

Если периметр треугольника, т. е. а + b + c обозначим для краткости через 2р, то получим

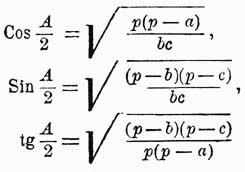
В этих формулах корень квадратный имеет значение положительное. Если s обозначает площадь треугольника, то s = 1/2(ab).Sinc или s = √[p(p — a)(p — b)(p — c)].

Если R радиус круга, описанного около треугольника, а r — радиус круга вписанного, то

R = a/(2SinA) = (abc)/(4s) и r = s/p.

Из перечисленных формул можно вывести другие при помощи перестановки букв. Напр., из формулы

а² = b² + с² — 2bc.CosA

следует

b² = а² + с² — 2ас. CosB.

При помощи указанных формул по данным частям треугольника вычисляются остальные его части. Подобная задача, называемая решением треугольников, встречается во многих практических вопросах: при геодезических съемках, при определении высот, при нахождении расстояния между неприступными точками и т. д.

Переходим теперь к треугольникам сферическим. Решение этих треугольников составляет предмет сферической тригонометрии. Предположим, что на поверхности шара радиуса R начерчен треугольник, вершины которого суть A, В и С. Соединив центр шара О с точками A, В и С, получим трехгранный угол, содержащий три плоских угла и три двугранных угла. Величины двугранных углов, ребра которых суть ОА, ОВ и ОС, обозначим через А, В и С, а величины противоположных им плоских углов через а, b и с. Будем предполагать, что шесть чисел А, В, С, а, b, с выражены в градусах, и что ни одно из них не превосходит 180°. Между этими числами имеют место следующие основные соотношения:

Cosa = Cosb.Cosc + Sinb. Sinc. CosA,

SinA/Sina = SinB/Sinb = SinC/Sinc

Cosa.Sinb — Sina.Cosb.CosC = Sinc.CosA,

Cosa.SinB — Cosb.CosC.SinA = CosA.Sin С,

Ctga. Sinb — CtgA.SinC = Cosb.CosC,

CosA = — CosB.CosC + SinB.SinC.Cosa.

Если a + b + c = 2p, то

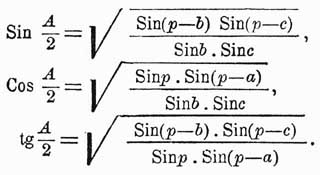
Сумма углов сферического треугольника содержит более 180°. Число A + В + С — 180° наз. сферическими избытком данного треугольника и обозначается буквою ε. Для определения числа градусов, содержащихся в одной из сторон сферического треугольника, углы которого даны, служат формулы

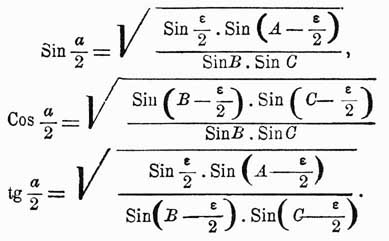
Площадь сферического треугольника равна (π/180)ε.R², где R радиус шара.

Формула Люилье (l'Huillier) дает возможность вычислить сферический избыток по сторонам треугольника.

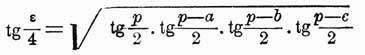
Укажем еще на формулы Деламбра:

Sin[(A + B)/2]:Cos[C/2] = Cos[(a — b)/2]:Cos[c/2]

Sin[(A — B)/2]:Cos[C/2] = Sin[(a — b)/2]:Sin[c/2]

Cos[(A + B)/2]:Sin[C/2] = Cos[(a + b)/2]:Cos[c/2]

Cos[(A — B)/2]:Sin[C/2] = Sin[(a + b)/2]:Sin[c/2]

и на формулы Непера:

tg[(A + B)/2] = (ctg[c/2])(Cos[(a — b)/2]/Cos[(a + b)/2])

tg[(A — B)/2] = (ctg[c/2])(Sin[(a — b)/2]/Sin[(a + b)/2])

tg[(a + b)/2] = (tg[c/2])(Cos[(A — B)/2]/Cos[(A + B)/2])

tg[(a — b)/2] = (tg[c/2])(Sin[(A — B)/2]/Sin[(A + B)/2])Из перечисленных формул получим новых при помощи перестановки букв.

Формулы сферической Т. очень часто применяются в астрономии.

Не перечисляя учебников тригонометрии, укажем на J. A. Serret, "Traité de Trigonométrie". Сведения по истории Т. можно найти в сочинении: Moritz Cantor, "Vorlesungen über Geschichte der Mathematik", доведенном до 1759 г. (до года рождения Лагранжа). Кроме того, в 1900 г. появилась первая часть сочинения: A. von Braunmühl, "Vorlesungen über Geschichte der Trigonometrie", в которой история Т. доведена до половины XVII стол. (до изобретения логарифмов).

Д. С.