РЕДЖЕ ПОЛЮСОВ МЕТОД

(комплексных угловых моментов метод), в квант. механике и в квант. теории поля (КТП) — метод описания и исследования рассеяния элем. ч-ц, основанный на формальном аналитич. продолжении парциальных амплитуд из области физ. значений момента кол-ва движения M=ћJ, J= 0, 1, 2, ..., в область комплексных значений J. Р. п. м. был введён итал. физиком Т. Редже (Т. Regge) при изучении аналитич. св-в квантовомеханич. амплитуды рассеяния. Матем. исследования процесса рассеяния показали, что резонансы и связанные состояния в амплитуде рассеяния появляются сериями, каждую из к-рых характеризует нек-рая функцион. зависимость между моментом I и квадратом массы (в энергетич. единицах) t:J=a(t). При этом резонансы данной серии возникают только при тех массах, для к-рых ф-ция a(t) равна целому неотрицат. числу (0, 1, 2, ...), выступающему как спин резонанса. Эта функцион. зависимость была названа т р а е к т о р и е й п о л ю с а Р е д ж е вследствие того, что в парциальной амплитуде рассеяния это явление описывается слагаемыми, имеющими вид полюса:

b(t)1/(J-a(t)), (1)

где b(t) — вычет полюса Редже. В области значений t, где a(t) действительна, целочисл. значения a(t) соответствуют стабильным связанным состояниям. При больших значениях t, превышающих границу сплошного спектра в задаче рассеяния (кинетич. энергия ч-цы ?кин>0), ф-ция a(t) становится комплексной: a(t)=Rea(t)+iIma(t) (где Re — действительная, Im — мнимая часть). В этом случае ф-ла (1) приобретает вид брейт-вигнеровского резонанса, причём Rea(t) продолжает определять положение теперь уже резонансного уровня, а Ima(t) оказывается пропорц. полной ширине уровня Г, т. е. определяет время жизни резонанса. Эта же ф-ция a(t) определяет и асимптотику продолжения амплитуды рассеяния в область больших нефиз. значений квадрата переданного четырёхмерного импульса (4-импульса) s (при фиксированном значении квадрата энергии t):

f(t,s)=b(t)(-s)a(t). (2)

В КТП Р. п. м. не имеет строгого теор. обоснования и используется как феноменологич. схема. В силу специфич. св-ва КТП — перекрёстной симметрии Р. п. м. приобретает более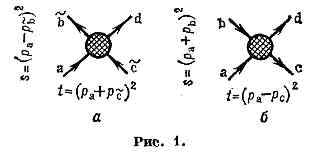

глубокое физ. содержание. Если амплитуду процесса а+с=®b=+d (рис. 1, а), зависящую от квадрата полной энергии в системе центра инерции (с. ц. и.) ч-ц а и с t=(pa+pc=)2 и квадрата передачи 4-импульса s= (ра-pb=)2, аналитически продолжить в область нефиз. больших значений s, то она описывает асимптотику перекрёстного процесса в s-канале, т. е. a+b®c+d c квадратом энергии в с. ц. и. s= (ра+рb)2 и квадратом передачи 4-импульса t=(ра-рс)2 (рис. 1,б). Отсюда следует, что в области больших энергий (s->1ГэВ2) дифф. сечение: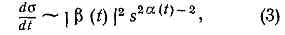

где a(t) — продолжение траектории Редже в физ. область процесса а+b®c+d (т. е. в область отрицат. квадратов масс t). Графически это изображается так, как будто ч-цы, рассеиваясь, обмениваются некой квазичастицей — т.н. реджеоном (R), спин к-рой зависит от передачи квадрата импульса (рис. 2).

Если частицы а и с обладают изотопическим спином (I), странностью (S), барионным зарядом (В) и т. д., то возможны неск. траекторий Редже, также различающихся этими квант. числами. Асимптотич. же поведение сечения процесса определяется передачей квант. чисел в t-канале (т. е. квант. чисел в системе ас) соответствующих самой верхней при t=0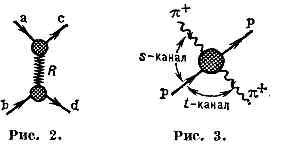

(«ведущей») траектории. Напр., процесс p+р-рассеяния назад, p++р®р+p+ (рис. 3), может идти как с передачей изотопич. спина DI=3/2, так и с DI=1/2, т. к. в перекрёстном t-канале в системе p-р существуют барионные резонансы с I=3/2 (D-реэонансы) и с I=1/2 (N-резонансы). Однако из опыта известно, что D-траектория лежит выше N-траектории (рис. 4), поэтому асимптотика процесса будет определяться именно траекторией D. Асимптотика же процесса перезарядки: p-+p®p°+n, к-рый идёт с DI=1, определяется обменом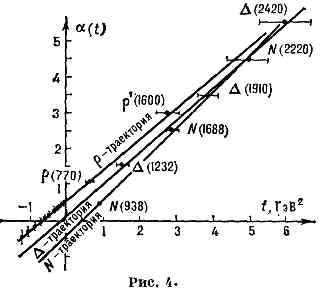

r-мезонной траекторией (рис. 4; там же показано, насколько хорошо «сшивается» траектория в области резонансов (t>0) и в области рассеяния (t<0)). Эксперим. точки в области t<0 получены в результате обработки по ф-ле (3) данных по перезарядке. Р. п. м. позволяет разбить все процессы с небольшой передачей импульса на неск. классов, отличающихся разной передачей квант. чисел и, следовательно, разной асимптотикой: а) процессы с обменом квант. числами вакуума (DI=0, DB=0 и т. д.) или с обменом т. н. особенностью Померанчука (к-рая не связана с к.-л. резонансами и, в отличие от других траекторий, не явл. полюсом; вопрос о её природе нельзя считать окончательно решённым). Эти процессы характеризуются постоянными (точнее, слабо растущими) сечениями. Примерами явл. все процессы упругого рассеяния. Этой же особенностью в соответствии с оптической теоремой (sполн =Imf(s, t=0)/s) определяется и поведение полных сечений.

б) Процессы с обменом мезонными траекториями (r, w, К*, p, h, К и др.). Сечения этих процессов с разной скоростью падают с ростом энергии в зависимости от того, какая из траекторий оказывается ведущей. К таким процессам относится рассмотренный выше процесс перезарядки.

в) Процессы с обменом барионными траекториями (напр., D, N, L, S). Сечения таких процессов также падают с ростом энергии.

г) Процессы с «экзотическим» обменом квант. числами (напр., DB=2 или DI=2), т. е. обменом такими квант. числами, к-рые не могут реализоваться в системе из кварка и антикварка или из трёх кварков (напр., р+р=®р=+р). Сечения их очень быстро падают с ростом энергии. Др. важное предсказание Р. п. м.— сужение дифракц. пика. Экспериментально известно, что сечение квазиупругих процессов а+b®с+d имеет резкий пик в области малых квадратов передач 4-импульса,?t?<0,1 (ГэВ/с)2 (дифракц. пик), и быстро падает с ростом ?t|. Это падение обычно апроксимируют экспоненц. зависимостью:

ds/dt»eB(t)f(s), (4)

а величину В называют наклоном дифракц. конуса. Если учесть, что в области малых 4 a(t)=a0+a'(t), где a0 — высота траектории при (=0, а a' — тангенс угла её наклона к оси t (это приближение оправдано, т. к. траектории Редже, как видно из рис. 4, почти прямолинейны), то ф-лу (3) можно привести к виду (4), причём величина В с увеличением энергии будет логарифмически расти: В (s)=B0+2a'lns, т. е. рассеянные ч-цы с ростом энергии сосредоточиваются во всё более узкой области передач импульса, так, как будто эфф. радиус r сталкивающихся ч-ц растёт: r2=r20+2a'lns (B0 и r0 — величина наклона и радиус при s=1ГэВ2). Это явление особенно чётко наблюдалось в процессах типа б — г (см., напр., эксперим. точки в области t<0 на рис. 4).

Р. п. м. нашёл широкое применение и в описании множественных процессов. В частности, в рамках этого метода естественно описываются такие явления, как скейлинг Фейнмана (см. МАСШТАБНАЯ ИНВАРИАНТНОСТЬ), корреляция двух вторичных ч-ц. Одна из загадок физики элем. ч-ц — наблюдаемая в эксперименте прямолинейность всех траекторий Редже и прибл. одинаковые их наклоны.