ДИАГРАММЫ ВЕННА
ДИАГРАММЫ ВЕННА – графический способ задания и анализа логико-математических теорий и их формул. Строятся путем разбиения части плоскости на ячейки (подмножества) замкнутыми контурами (кривыми Жордана). В ячейках представляется информация, характеризующая рассматриваемую теорию или формулу. Цель построения диаграмм не только иллюстративная, но и операторная – алгоритмическая переработка информации. Аппарат диаграмм Венна обычно используется вместе с аналитическим.
Способ разбиения, количество ячеек, а также проблемы записи в них информации зависят от рассматриваемой теории, которая тоже может вводиться (описываться) графически – некоторыми диаграммами Венна, задаваемыми первоначально, в частности, вместе с алгоритмами их преобразований, когда одни диаграммы могут выступать как операторы, действующие на другие диаграммы. Напр., в случае классической логики высказываний [ЛОГИКА ВЫСКАЗЫВАНИЙ] для формул, составленных из n различных пропозициональных переменных, часть плоскости (универсум) делится на 2n ячеек, соответствующих конституэнтам (в конъюнктивной или в дизъюнктивной форме). Диаграммой Венна каждой формулы считается такая плоскость, в ячейках которой ставится (или не ставится) звездочка *. Так, формулу
( а&
а& b&с) ∨(a&
b&с) ∨(a& b&c) ∨ (
b&c) ∨ ( a&b&
a&b& c)
c)
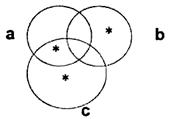
с тремя пропозициональными переменными a, b и с определяет диаграмма, изображенная на рисунке, где звездочки в ячейках соответствуют конъюнктивным составляющим этой совершенной нормальной дизъюнктивной формулы. Если отмеченных звездочками ячеек нет, то диаграмме Венна сопоставляется, напр., тождественно ложная формула, скажем, (a& a).
a).
Индуктивный способ разбиения плоскости на 2n ячеек восходит к трудам английского логика Дж. Венна, называется способом Венна и состоит в следующем:
1. При n = 1, 2, 3 очевидным образом используются окружности. (На приведенном рисунке n = 3.)
2. Предположим, что при n = k (k≥3), указано такое расположение k фигур, что плоскость разделена на 2k ячеек. Тогда для расположения k + 1 фигуры на этой плоскости достаточно, во-первых, выбрать незамкнутую кривую φ без точек самопересечения, т.е. незамкнутую кривую Жордана, принадлежащую границам всех 2k ячеек и имеющую с каждой из этих границ только один общий кусок. Во-вторых, обвести φ замкнутой кривой Жордана ψk+1, так, чтобы кривая ψk+1 проходила через все 2k ячейки и пересекала границу каждой ячейки только два раза.
Т.о. получится расположение n=k+l фигур такое, что плоскость разделится на 2k+1 ячеек.
Для представления других логико-математических теорий метод венновских диаграмм расширяется. Сама теория записывается так, чтобы выделить элементы ее языка в пригодной для графического изображения форме. Напр., атомарные формулы классической логики предикатов [ЛОГИКА ПРЕДИКАТОВ] записываются как слова вида P(y1...yr), где Р – предикатная, a y1, …, уr – предметные переменные, не обязательно различные; слово y1... yr – предметный инфикс. Очевидный теоретико-множественный характер диаграмм Венна позволяет представлять и исследовать с их помощью, в частности, теоретико-множественные исчисления, напр., исчисление ZF теории множеств Цермело-Френкеля.
Графические методы в логике и математике развивались издавна. Таковы, в частности, логический квадрат, круги Эйлера и оригинальные диаграммы Л.Кэрролла [КЭРРОЛЛ]. Однако метод диаграмм Венна существенно отличается от известного метода кругов Эйлера, используемого в традиционной силлогистике [СИЛЛОГИСТИКА]. В основе венновских диаграмм лежит идея разложения булевской функции на конституэнты – центральная в алгебре логики [АЛГЕБРА ЛОГИКИ], обуславливающая их оперативный характер. Свои диаграммы Венн применял прежде всего для решения задач логики классов. Его диаграммы можно эффективно использовать и для решения задач логики высказываний и предикатов, обзора следствий из посылок, решения логических уравнений, а также других вопросов, вплоть до проблемы разрешимости. Аппарат диаграмм Венна находит применение в приложениях математической логики и теории автоматов, в частности при решении задач, связанных с нейронными цепями и проблемой синтеза надежных схем из относительно мало надежных элементов.
Литература:
1. Venn J. Symbolic logic. L., 1881. Ed. 2, rev. L., 1894;
2. Кузичев А.С. Диаграммы Венна. История и применения. М., 1968;
3. Он же. Решение некоторых задач математической логики с помощью диаграмм Венна. – В кн.: Исследование логических систем. М., 1970.
А.С.Кузичев
