Ритца и Галёркина методы

Ри́тца и Галёркина методы

Широко распространённые Прямые методы решения главным образом вариационных задач и краевых задач математического анализа (см. Краевые задачи, Вариационное исчисление).

Метод Ритца применяется большей частью для приближённого решения вариационных задач и тех краевых задач, которые сводятся к вариационным. Пусть задан Функционал V [y (x)] (или более сложный функционал) и требуется найти такую функцию у (х), принимающую в точках x₀ и x_i заданные значения α = у (х₀) и β = у (х₁), на которой функционал V [y (x)] будет достигать Экстремума. Значения исследуемого на экстремум функционала V [y (x)] рассматриваются не на всех допустимых в данной задаче функциях у (х), а лишь на всевозможных линейных комбинациях вида

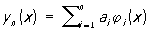
с постоянными коэффициентами a_i, составленных из n первых функций некоторой выбранной системы φ₁(x), φ₂(х),..., φ_п (х),... (от удачного выбора этой системы функций зависит эффективность применения метода к решению конкретных задач). Необходимым условием выбора системы функций φ₁(х) является требование, чтобы функции у_п (х) удовлетворяли условиям уп (х_о) = α и y_n (x₁) = α для всех значений параметров a_1. При таком выборе функций у_п (х) функционал V [y (x)] превращается в функцию Ф (а₁, a₂,..., a_n) коэффициентов a_i, последние выбирают так, чтобы эта функция достигала экстремума, т. е. определяют их из системы уравнений

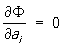(i=1, 2, ..., n).

Например, пусть требуется решить задачу о минимуме интеграла

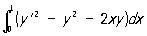
при условии y (0) = y (1) = 0. В качестве функций φ_i (x) можно взять xⁱ (1 — х), тогда

.

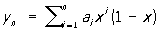Если n = 2, то 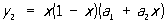. Для определения коэффициентов a₁ и a₂ получаем после вычислений два уравнения

;

.

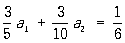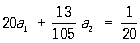Решением этих уравнений являются числа a₁ = 71/369 и a₂ = ⁷/₄₁. Следовательно, 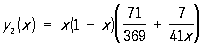. Полученное приближённое решение отличается от точного на величину порядка 0,001.

Найденное этим методом приближённое решение у_п (х) вариационной задачи при некоторых условиях, касающихся в основном полноты системы функций φ_i (x), стремится к точному решению у (х), когда n → ∞.

Метод был предложен в 1908 немецким математиком В. Ритцем (W. Ritz). Теоретическое обоснование метода дано сов. математиком Н. М. Крыловым (1918).

Метод Галёркина является широким обобщением метода Ритца и применяется главным образом для приближённого решения вариационных и краевых задач, в том числе и тех, которые не сводятся к вариационным. Основная идея метода Галёркина состоит в следующем. Пусть требуется в некоторой области D найти решение дифференциального уравнения

L [u] = 0 (1)

(L — некоторый дифференциальный оператор, например по двум переменным), удовлетворяющее на границе S области D однородным краевым условиям:

u = 0. (2)

Если функция u является решением уравнения (1) в области D, то функция L [u] тождественно равна нулю в этой области и, следовательно, ортогональна (см. Ортогональность) любой функции в области D. Приближённое решение уравнения (1) ищут в виде

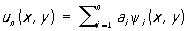, (3)

где ψ_i (x, y) (i = 1, 2,..., n) — линейно независимые функции, удовлетворяющие краевым условиям (2) и являющиеся первыми n функциями некоторой системы функций ψ₁(x, у), ψ₂(х, у),..., ψ_п (х, у),..., полной в данной области. Постоянные коэффициенты a_i выбирают так, чтобы функция L [u_n] была ортогональна в D первым n функциям системы ψ_i (x, y):

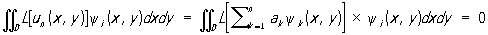(4)

(i=1, 2, ..., n).

Например, пусть в области D требуется решить уравнение Пуассона

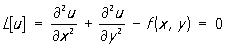
при условии u = 0 на S. Выбирая систему функций ψ_i (x, y), ищем решение в виде (3). Система уравнений (4) для определения коэффициентов ai имеет вид:

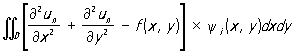
(i=1, 2, ..., n).

Функции ψ_i (x, y) можно, в частности, выбирать, пользуясь следующими соображениями. Пусть ω(x, y) — непрерывная функция, имеющая внутри области D непрерывные частные производные второго порядка и такая, что ω(x, y) > 0 внутри D, ω(x, y) = 0 на S. Тогда в качестве системы функций ψ_i (x, y) можно взять систему, составленную из произведений ω(x, y) на различные степени х и y: 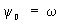, , 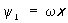, , 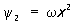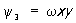… Например, если границей области D является окружность S радиуса R с центром в начале координат, то можно положить ω(x, y) = R² — x² — y².

Метод Галёркина применяется при решении широкого класса задач; более общая его формулировка даётся в терминах функционального анализа (См. Функциональный анализ) для решения уравнений вида Au — f = 0, где А — линейный оператор, определённый на линеале, плотном в некотором гильбертовом пространстве H, u — искомый и f — заданный элементы пространства H.

Метод получил распространение после исследований Б. Г. Галёркина (1915); ранее (1913) он применялся для решения конкретных задач теории упругости И. Г. Бубновым, в связи с чем иногда именуется методом Бубнова — Галёркина. Теоретическое обоснование метода принадлежит М. В. Келдышу (1942).

Лит.: Галёркин Б. Г., Стержни и пластинки. Ряды в некоторых вопросах упругого равновесия стержней и пластинок, «Вестник инженеров», 1915, т. 1, № 19, с. 897—908; Михлин С. Г., Вариационные методы в математической физике, 2 изд., М. — Л., 1970; Канторович Л. В. и Крылов В. И., Приближённые методы высшего анализа, 5 изд., Л. — М., 1962; Ritz W., Neue Methode zur Lösung gewisser Randwertaufgaben, «Gesellschaft der Wissenschaften zu Göttingen. Math.-physik. Klasse. Nachrichten», Göttingen, 1908; его же, Über еще neue Methode zur Lösung gewisser Variationsprobleme der mathematischen Physik, «Journal für die reine und angewandte Mathematik», 1909, Bd 135.

В. Г. Карманов.