Неопределённые выражения

Неопределённые выраже́ния

В математике, выражения, Предел которых не может быть найден путём непосредственного применения теорем о пределах. Типы Н. в.:

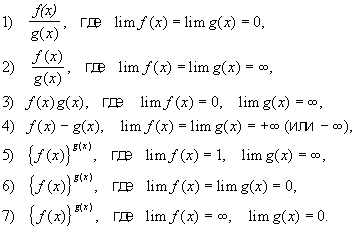
К Н. в. относятся:

причём

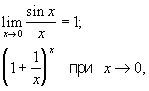
причём

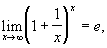
где e = 2,71828... — Неперово число. Указанные типы Н. в. символически обозначают так:

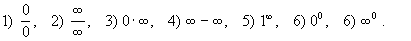
Следует отметить, что данная функция может являться Н. в. при одних значениях аргумента и не являться таковым при других (например, выражение

не является Н. в.). Не всякое Н. в. имеет предел; так, выражение

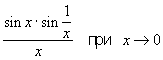
не стремится ни к какому пределу

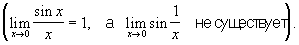
Нахождение предела Н. в. (в случае, когда он существует) называют иногда «раскрытием неопределённости», или нахождением «истинного значения» Н. в. (второй термин устарел). Оно часто основывается на замене данной функции другой, имеющей тот же предел, но не являющейся уже Н. в. Иногда такая замена достигается путём алгебраических преобразований.

Так, например, сокращая в выражении

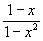
числитель и знаменатель на 1—x, получаем

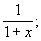
поэтому

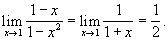
Для вычисления пределов Н. в. типов 1) и 2) часто оказывается полезной теорема (или правило) Лопиталя, утверждающая, что в этих случаях

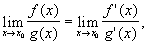
если f (x) и g (x) дифференцируемы в окрестности (конечной или бесконечно удалённой) точки x₀, за возможным исключением самой точки x₀, и второй предел существует. Пользуясь этой теоремой, находим, например, что

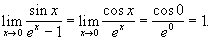
Иногда

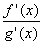
вновь является Н. в. вида 1) или 2); тогда теорема Лопиталя может быть применена (при выполнении её условий) ещё раз и т. д. Однако это не всегда приводит к цели: например, применение теоремы Лопиталя к Н. в.

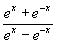
[f (x) = e^x + e^-x, g (x) = e^x — e^-x]при x → 0 ничего не даёт. Может также случиться, что

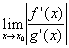
не существует, тогда как

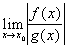
типа 1) или 2) всё же существует; пример:

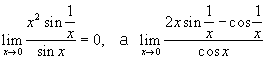
не существует. Мощным средством нахождения пределов Н. в. является разложение функций в ряды. Например, так как

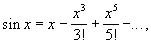
то

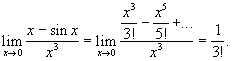
Н. в. видов 3)—7) могут быть сведены к одному из видов 1) или 2). Так, например, при х → π/2 Н. в.

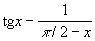
вида 4) преобразуется к виду 1):

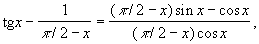
а последнее Н. в. имеет предел 0; Н. в. вида 3) приводится к Н. в. вида 1) или 2) преобразованием

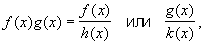
где

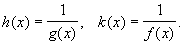
Наконец, если через u (х) обозначить логарифм Н. в. видов 5), 6) и 7): u (x) = g (x) lnf (x), то u (х) является Н. в. вида 3), которое, как указано, сводится к Н. в. вида 1) или 2). Так как {f (x)} ^{g (x)} = e^{u (x)}, то, найдя предел u (х) (если он существует), можно найти и предел данного Н. в. Например, для x^x при x → 0 имеем

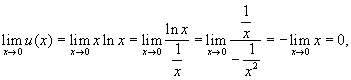
и, следовательно,

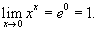
Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1, М., 1973.