статистическая термодинамика

СТАТИСТИЧЕСКАЯ ТЕРМОДИНАМИКА

раздел статистич. физики, посвященный обоснованию законов термодинамики на основе законов взаимод. и движения составляющих систему частиц. Для систем в равновесном состоянии С. т. позволяет вычислять термодинамические потенциалы, записывать уравнения состояния, условия фазовых и хим. равновесий. Неравновесная С. т. дает обоснование соотношений термодинамики необратимых процессов (уравнений переноса энергии, импульса, массы и их граничных условий) и позволяет вычислять входящие в уравнения переноса кинетич. коэффициенты. С. т. устанавливает количеств. связь между микро- и макросвойствами физ. и хим. систем. Расчетные методы С. т. используются во всех направлениях совр. теоретич. химии.

Основные понятия. Для статистич. описания макроскопич. систем Дж. Гиббсом (1901) предложено использовать понятия статистич. ансамбля и фазового пространства, что позволяет применять к решению задач методы теории вероятности. Статистич. ансамбль-совокупность очень большого числа одинаковых систем мн. частиц (т. е. "копий" рассматриваемой системы), находящихся в одном и том же макросостоянии, которое определяется параметрами состояния; микросостояния системы при этом могут различаться. Осн. статистич. ансамбли-микроканонич., канонич., большой канонич. и изобарно-изотермический.

Микроканонич. ансамбль Гиббса используетя при рассмотрении изолированных систем (не обменивающихся энергией E с окружающей средой), имеющих постоянный объем V и число одинаковых частиц N (Е, V и N- параметры состояния системы). Канонич. ансамбль Гиббса используется для описания систем постоянного объема, находящихся в тепловом равновесии с окружающей средой (абс. температура Т) при постоянном числе частиц N (параметры состояния V, Т, N). Большой канонич. ансамбль Гиббса используется для описания открытых систем, находящихся в тепловом равновесии с окружающей средой (температура Т) и материальном равновесии с резервуаром частиц (осуществляется обмен частицами всех сортов через "стенки", окружающие систему объемом V). Параметры состояния такой системы-V, Т и m—химический потенциал частиц. Изобарно-изотермич. ансамбль Гиббса используется для описания систем, находящихся в тепловом и мех. равновесии с окружающей средой при постоянном давлении P (параметры состояния Т, P, N).

Фазовое пространство в статистич. механике-многомерное пространство, осями которого служат все обобщенные координаты q_i и сопряженные им импульсы p_i(i =1,2,..., М) системы с М степенями свободы. Для системы, состоящей из N атомов, q_i и p_i соответствуют декартовой координате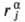и компоненте импульса 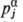(α = х, у, z) некоторого атома j и М = 3N. Совокупность координат и импульсов обозначаются q и p соответственно. Состояние системы изображается точкой в фазовом пространстве размерности 2М, а изменение состояния системы во времени-движением точки вдоль линии, наз. фазовой траекторией. Для статистич. описания состояния системы вводятся понятия фазового объема (элемента объема фазового пространства) и функции распределения f(p, q), которая характеризует плотность вероятности нахождения точки, изображающей состояние системы, в элементе фазового пространства вблизи точки с координатами р, q. В квантовой механике вместо фазового объема используют понятие дискретного энергетич. спектра системы конечного объема, т. к. состояние отдельной частицы определяется не импульсом и координатами, а волновой функцией, которой в стационарном динамич. состоянии системы соответствует энергетич. спектр квантовых состояний.

Функция распределения классич. системы f(p, q) характеризует плотность вероятности реализации данного микросостояния (р, q) в элементе объема dГ фазового пространства. Вероятность пребывания N частиц в бесконечно малом объеме фазового пространства равна:

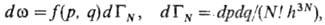
где dГ_N — элемент фазового объема системы в единицах h^3N, h-постоянная Планка; делитель N! учитывает тот факт, что перестановка тождеств. частиц не меняет состояния системы. Функция распределения удовлетворяет условию нормировки тf(p, q)dГ_N= 1, т. к. система достоверно находится в к.-л. состоянии. Для квантовых систем функция распределения определяет вероятность w_{i∞ N} нахождения системы из N частиц в квантовом состоянии, задаваемом набором квантовых чисел i, с энергией E_i,N при условии нормировки

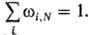
Среднее значение 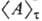в момент времени т (т. е. по бесконечно малому интервалу времени от т до т + dт) любой физ. величины А(р, q), являющейся функцией координат и импульсов всех частиц системы, с помощью функции распределения вычисляется по правилу (в т. ч. и для неравновесных процессов):

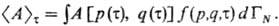
Интегрирование по координатам проводится по всему объему системы, а интегрирование по импульсам от −, до +,. Состояние термодинамич. равновесия системы следует рассматривать как предел т:,. Для равновесных состояний функции распределения определяются без решения уравнения движения составляющих систему частиц. Вид этих функций (одинаковый для классич. и квантовых систем) был установлен Дж. Гиббсом (1901).

В микроканонич. ансамбле Гиббса все микросостояния с данной энергией Е равновероятны и функция распределения для классич. систем имеет вид:

f(p,q) = Ad[H(p,q)-E],

где d-дельта-функция Дирака, Н(р,q)-функция Гамильтона, представляющая собой сумму кинетич. и потенц. энергий всех частиц; постоянная А определяется из условия нормировки функции f(p, q). 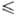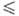Для квантовых систем при точности задания квантового состояния, равной величине ΔE, в соответствии с соотношением неопределенностей между энергией и временем (между импульсом и координатой частицы), функция w(E_k) = [g(E, N, V)]⁻¹, если ЕE_kE + ΔE, и w(E_k) = 0, если E_k < Е и E_k > E + ΔE. Величина g(E, N, V) — т. наз. статистич. вес, равный числу квантовых состояний в энергетич. слое ΔE. Важное соотношение С. т. — связь энтропии системы со статистич. весом:

S(E, N, V) = klng(E, N, V), где k-Больцмана постоянная.

В канонич. ансамбле Гиббса вероятность нахождения системы в микросостоянии, определяемом координатами и импульсами всех N частиц или значениями E_i,N, имеет вид: f(p, q) = exp {[F — H(p, q)]/kT}; w_i,N = exp[(F — E_i,N)/kT], где F — своб. энергия (энергия Гельмгольца), зависящая от значений V, Т, N:

F = -kTlnZ_N,

где Z_N-статистич. сумма (в случае квантовой системы) или статистич. интеграл (в случае классич. системы), определяемые из условия нормировки функций w_i,N или f(p, q):

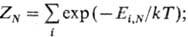
Z_N = тexp[-H(р, q)/kT]dpdq/(N!h^3N)

(сумма по г берется по всем квантовым состояниям системы, а интегрирование проводится по всему фазовому пространству).

В большом канонич. ансамбле Гиббса функция распределения f(p, q) и статистич. сумма X, определяемая из условия нормировки, имеют вид:

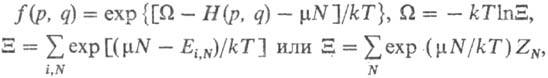
где W-термодинамич. потенциал, зависящий от переменных V, Т, m (суммирование ведется по всем целым положит. N). В изобарно-изотермич. ансамбле Гиббса функция распределения и статистич. сумма Q, определяемая из условия нормировки, имеют вид:

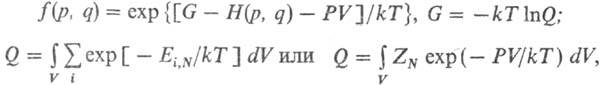
где G — энергия Гиббса системы (изобарно-изотермич. потенциал, своб. энтальпия).

Для вычисления термодинамич. функции можно использовать любое распределение: они эквивалентны друг другу и соответствуют разным физ. условиям. Микроканонич. распределение Гиббса применяется гл. обр. в теоретич. исследованиях. Для решения конкретных задач рассматривают ансамбли, в которых есть обмен энергией со средой (канонич. и изобарно-изотермич.) или обмен энергией и частицами (большой канонич. ансамбль). Последний особенно удобен для изучения фазового и хим. равновесий. Статистич. суммы Z_N и Q позволяют определить энергию Гельмгольца F, энергию Гиббса G, а также термодинамич. свойства системы, получаемые дифференцированием статистич. суммы по соответствующим параметрам (в расчете на 1 моль вещества): внутр. энергию U = RT²(9lnZ_N/9T)_V, энтальпию H = RT²(9lnQ/9T)_P, энтропию S = RlnZ_N + RT(9lnZ_N/9T)_V = = R ln Q + RT(9ln Q/9T)_P, теплоемкость при постоянном объеме C_V = 2RT(9lnZ_N/9T)_V + RT²(9² lnZ_N/9T²)_V, теплоемкость при постоянном давлении C_Р = 2RT (9lnZ_N/9T)_P + RT²(9²lnZ_N/9T²)_P и т. д. Соотв. все эти величины приобретают и статистич. смысл. Так, внутренняя энергия отождествляется со средней энергией системы, что позволяет рассматривать первое начало термодинамики как закон сохранения энергии при движении составляющих систему частиц; своб. энергия связана со статистич. суммой системы, энтропия — с числом микросостояний g в данном макросостоянии, или статистич. весом макросостояния, и, следовательно, с его вероятностью. Смысл энтропии как меры вероятности состояния сохраняется по отношению к произвольным (неравновесным) состояниям. В состоянии равновесия энтропия изолир. системы имеет максимально возможное значение при заданных внеш. условиях (Е, V, N), т. е. равновесное состояние является наиб. вероятным состоянием (с макс. статистич. весом). Поэтому переход из неравновесного состояния в равновесное есть процесс перехода из менее вероятных состояний в более вероятное. В этом заключается статистич. смысл закона возрастания энтропии, согласно которому энтропия замкнутой системы может только увеличиваться (см. второе начало термодинамики). При температуре абс. нуля любая система находится в осн. состоянии, в котором w₀ = 1 и S = 0. Это утверждение представляет собой третье начало термодинамики (см. тепловая теорема). Существенно, что для однозначного определения энтропии нужно пользоваться квантовым описанием, т. к. в классич. статистике энтропия м. б. определена только с точностью до произвольного слагаемого.

Идеальные системы. Расчет статистич. сумм большинства систем представляет сложную задачу. Она существенно упрощается в случае газов, если вкладом потенц. энергии в полную энергию системы можно пренебречь. В этом случае полная функция распределения f(p, q) для N частиц идеальной системы выражается через произведение одно-частичных функций распределения φ₁(p, q):

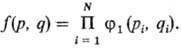
Распределение частиц по микросостояниям зависит от их кинетич. энергии и от квантовых свойств системы, обусловленных тождественностью частиц. В квантовой механике все частицы разделяются на два класса: фермионы и бозоны. Тип статистики, которой подчиняются частицы, однозначно связан с их спином.

Статистика Ферми-Дирака описывает распределение в системе тождеств. частиц с полуцелым спином ¹/₂, ³/₂,... в единицах ђ = h/2π. Частица (или квазичастица), подчиняющаяся указанной статистике, наз. фермионом. К фер-мионам относятся электроны в атомах, металлах и полупроводниках, атомные ядра с нечетным атомным номером, атомы с нечетной разностью атомного номера и числа электронов, квазичастицы (напр., электроны и дырки в твердых телах) и т. д. Данная статистика была предложена Э.Ферми в 1926; в том же году П.Дирак выяснил ее квантовомех. смысл. Волновая функция системы фермионов антисимметрична, т. е. меняет свой знак при перестановке координат и спинов любой пары тождеств. частиц. В каждом квантовом состоянии может находиться не более одной частицы (см. Паули принцип). Среднее число частиц n_i идеального газа фермионов, находящихся в состоянии с энергией E_i∞ определяется функцией распределения Ферми-Дирака:

n_i={1+exp[(E_i-m)/kT]}⁻¹,

где i — набор квантовых чисел, характеризующих состояние частицы.

Статистика Бозе-Эйнштейна описывает системы тождеств. частиц с нулевым или целочисленным спином (0, ђ, 2ђ, ...). Частица или квазичастица, подчиняющаяся указанной статистике, наз. бозоном. Данная статистика была предложена Ш. Бозе (1924) для фотонов и развита А. Эйнштейном (1924) применительно к молекулам идеального газа, рассматриваемым как составные частицы из четного числа фермионов, напр. атомные ядра с четным суммарным числом протонов и нейтронов (дейтрон, ядро ⁴Не и т. д.). К бозонам относятся также фононы в твердом теле и жидком ⁴Не, экситоны в полупроводниках и диэлектриках. Волновая функция системы симметрична относительно перестановки любой пары тождеств. частиц. Числа заполнения квантовых состояний ничем не ограничены, т. е. в одном состоянии может находиться любое число частиц. Среднее число частиц n_i идеального газа бозонов, находящихся в состоянии с энергией Е_i описывается функцией распределения Бозе-Эйнштейна:

n_i={exp[(E_i-m)/kT]-1}⁻¹.

Статистика Больцмана представляет собой частный случай квантовой статистики, когда можно пренебречь квантовыми эффектами (высокие температуры). В ней рассматривается распределение частиц идеального газа по импульсам и координатам в фазовом пространстве одной частицы, а не в фазовом пространстве всех частиц, как в распределениях Гиббса. В качестве миним. единицы объема фазового пространства, имеющего шесть измерений (три координаты и три проекции импульса частицы), в соответствии с квантовомех. соотношением неопределенностей, нельзя выбрать объем меньший, чем h³. Среднее число частиц n_i идеального газа, находящихся в состоянии с энергией E_i, описывается функцией распределения Больцмана:

n_i=exp[(m-E_i)/kT].

Для частиц, которые движутся по законам классич. механики во внеш. потенц. поле U(r), статистически равновесная функция распределения φ₁(p,r) по импульсам p и координатам r частиц идеального газа имеет вид: φ₁(p,r) = A ехр{ — [р²/2m + U(r)]/kT}. Здесь р²/2т-кинетич. энергия молекул массой ш, постоянная А определяется из условия нормировки. Данное выражение часто наз. распределением Максвелла-Больцмана, а распределением Больцмана наз. функцию

n(r) = n₀ ехр[-U(r)]/kT],

где n(r) = тφ₁(p, r)dp — плотность числа частиц в точке r (n₀-плотность числа частиц в отсутствие внеш. поля). Распределение Больцмана описывает распределение молекул в поле тяготения (барометрич. формула), молекул и высокодисперсных частиц в поле центробежных сил, электронов в невырожденных полупроводниках, а также используется для расчета распределения ионов в разбавл. растворах электролитов (в объеме и на границе с электродом) и т. п. При U(r) = 0 из распределения Максвелла — Больц-мана следует распределение Максвелла, описывающее распределение по скоростям частиц, находящихся в ста-тистич. равновесии (Дж. Максвелл, 1859). Согласно этому распределению, вероятное число молекул в единице объема 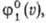компоненты скоростей которых лежат в интервалах от u_i до u_i + du_i (i = x, у, z), определяется функцией:

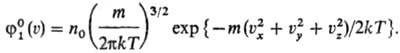
Распределение Максвелла не зависит от взаимод. между Частицами и справедливо не только для газов, но и для жидкостей (если для них возможно классич. описание), а также для броуновских частиц, взвешенных в жидкости и газе. Его используют для подсчета числа столкновений молекул газа между собой в ходе хим. реакции и с атомами поверхности.

Сумма по состояниям молекулы. Статистич. сумма идеального газа в канонич. ансамбле Гиббса выражается через сумму по состояниям одной молекулы Q₁:

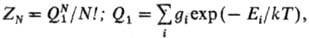
где Е_i — энергияi-го квантового уровня молекулы (i = О соответствует нулевому уровню молекулы), g_i-статистич. вес i-го уровня. В общем случае отдельные виды движения электронов, атомов и групп атомов в молекуле, а также движение молекулы как целого взаимосвязаны, однако приближенно их можно рассматривать как независимые. Тогда сумма по состояниям молекулы м. б. представлена в виде произведения отдельных составляющих, связанных с по-ступат. движением (Q_пост) и с внутримол. движениями (Q_вн):

Q₁ = Q_пост∙Q_вн, Q_пост= λ(V/N),

где λ = (2πmkТ/h²)^3/2. Для атомов Q_вн представляет собой сумму по электронным и ядерным состояниям атома; для молекул Q_вн- сумма по электронным, ядерным, колебат. и вращат. состояниям. В области температур от 10 до 10³ К обычно используют приближенное описание, в котором каждый из указанных типов движения рассматривается независимо: Q_вн = Q_эл∙Q_яд∙Q_вращ∙Q_кол/γ, где γ — число симметрии, равное числу тождество. конфигураций, возникающих при вращении молекулы, состоящей из одинаковых атомов или групп атомов.

Сумма по состояниям электронного движения Q_эл равна статистич. весу Р_т осн. электронного состояния молекулы. Во мн. случаях осн. уровень невырожден и отделен от ближайшего возбужденного уровня значит. энергией: (Р_т = 1). Однако в ряде случаев, напр. для молекулы O₂, Р_т = з, в осн. состоянии момент количества движения молекулы отличен от нуля и имеет место вырождение энергетических уровней, а энергии возбужденных состояний м. б. достаточно низкими. Сумма по состояниям Q_яд, обусловленная вырождением ядерных спинов, равна:

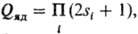
где s_i-спин ядра атома i, произведение беретсяпо всем атомам молекулы. Сумма по состояниям колебат. движения молекулы где v_i-частоты нормальных колебаний, 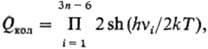n-число атомов в молекуле. Сумму по состояниям вращат. движений многоатомной молекулы с большими моментами инерции можно рассматривать классически [высокотемпературное приближение, T/q_i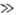1, где q_i = h²/8π²kI_i (i = x, у, z), I_t-главный момент инерции вращения вокруг оси i]: Q_вр = (πT³/q_xq_yq_z)^1/2. Для линейных молекул с моментом инерции I статистич. сумма Q_вр = T/q, где q = h²/8π²*kI.

При расчетах при температурах выше 10³К необходимо учитывать ангармонизм колебаний атомов, эффекты взаимод. колебат. и вращат. степеней свободы (см. нежесткие молекулы), а также мультиплетности электронных состояний, заселенности возбужденных уровней и т. д. При низких температурах (ниже 10 К) необходимо учитывать квантовые эффекты (особенно для двухатомных молекул). Так, вращат. движение гетеро-ядерной молекулы АВ описывается по формуле:

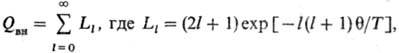
l-номер вращат. состояния, а для гомоядерных молекул А₂(особенно для молекул водорода H₂, дейтерия D₂, трития Т₂) ядерные и вращат. степени свободы взаимод. друг с другом: Q_яд._вращ. Q_яд∙Q_вращ.

Знание суммы по состояниям молекулы позволяет рассчитать термодинамич. свойства идеального газа и смеси идеальных газов, в т. ч. константы хим. равновесия, равновесную степень ионизации и т. п. Важное значение в теории абс. скоростей реакций имеет возможность расчета константы равновесия процесса образования активир. комплекса (переходного состояния), которое представляется как модифицир. частица, одна из колебат. степеней свободы которой заменена степенью свободы поступат. движения.

Неидеальные системы. В реальных газах молекулы взаимод. друг с другом. В этом случае сумма по состояниям ансамбля не сводится к произведению сумм по состояниям отдельных молекул. Если считать, что межмол. взаимод. не влияют на внутр. состояния молекул, статистич. сумма системы в классич. приближении для газа, состоящего из N тождеств. частиц, имеет вид:

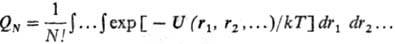
где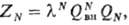

Здесь <2_N-конфигурац. интеграл, учитывающий взаимод. молекул. Наиб. часто потенц. энергия молекул U рассматривается в виде суммы парных потенциалов: U = =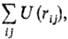где U(r_ij)- потенциал центр. сил, зависящий от расстояния r_ij между молекулами i и j. Учитывают также многочастичные вклады в потенц. энергию, эффекты ориентации молекул и т. д. Необходимость расчета конфигурац. интеграла возникает при рассмотрении любых конденсир. фаз и границ раздела фаз. Точное решение задачи мн. тел практически невозможно, поэтому для расчета статистич. суммы и всех термодинамич. свойств, получаемых из статистич. суммы дифференцированием по соответствующим параметрам, используют разл. приближенные методы.

Согласно т. наз. методу групповых разложений, состояние системы рассматривается в виде совокупности комплексов (групп), состоящих из разного числа молекул, и конфигурац. интеграл распадается на совокупность групповых интегралов. Такой подход позволяет представить любую термодинамич. функцию реального газа в виде ряда по степеням плотности. Наиб. важное соотношение такого рода — вириальное уравнение состояния.

Для теоретич. описания свойств плотных газов, жидкостей и твердых тел, растворов неэлектролитов и электролитов и границ раздела в этих системах более удобным, чем прямой расчет статистич. суммы, является метод n-частичных функций распределения. В нем вместо подсчета статистич. веса каждого состояния с фиксир. энергией используют соотношения между функциями распределения φ_n, которые характеризуют вероятность нахождения частиц одновременно в точках пространства с координатами r₁,..., r_n; при n = N φ_N = b тf(p, r)dp (здесь и ниже q_i = r_i). Одночастичная функция φ₁(r₁) (n = 1) характеризует распределение плотности вещества. Для твердого тела это периодич. функция с максимумами в узлах кристаллич. структуры; для газов или жидкостей в отсутствие внеш. поля это постоянная величина, равная макроскопич. плотности вещества р. Двухчастичная функция распределения (n = 2) характеризует вероятность нахождения двух частиц в точках 1 и 2, она определяет т. наз. корреляционную функцию g(|r₁ — r₂|) = φ₂(r₁, r₂)/ρ², характеризующую взаимную корреляцию в распределении частиц. Соответствующую опытную информацию дает рентгеновский структурный анализ.

Функции распределения размерности n и n + 1 связаны бесконечной системой зацепляющихся интегродифференц. уравнений Боголюбова — Борна — Грина-Кирквуда-Ивона, решение которых чрезвычайно сложно, поэтому эффекты корреляции между частицами учитывают введением разл. аппроксимаций, которые определяют, каким бразом функция φ_n выражается через функции меньшей размерности. Соотв. разработано неск. приближенных методов расчета функций φ_n, а через них-всех термодинамич. характеристик рассматриваемой системы. Наиб. применение имеют приближения Перкус — Иевика и гиперцепное.

Решеточные модели конденсир. состояния нашли широкое применение при термодинамич. рассмотрении практически всех физ.-хим. задач. Весь объем системы разбивается на локальные области с характерным размером порядка размера молекулы u₀. В общем случае в разных моделях размер локальной области м. б. как больше, так и меньше u₀; в большинстве случаев они совпадают. Переход к дискретному распределению молекул в пространстве существенно упрощает подсчет разл. конфигураций молекул. Решеточные модели учитывают взаимод. молекул друг с другом; энергия взаимод. описывается энергетич. параметрами. В ряде случаев решеточные модели допускают точные решения, что позволяет оценить характер используемых приближений. С их помощью возможно рассмотрение многочастичных и специфич. взаимод., ориентац. эффектов и т. п. Решеточные модели являются основными при изучении и проведении прикладных расчетов растворов неэлектролитов и полимеров, фазовых переходов, критических явлений, сильно неоднородных систем.

Численные методы определения термодинамич. свойств приобретают все большее значение по мере развития вычислит. техники. В методе Монте — Карло осуществляется прямой расчет многомерных интегралов, что позволяет непосредственно получить статистич. среднее наблюдаемой величины А(r1.....r_N) по любому из статистич. ансамблей (напр., А — энергия системы). Так, в канонич. ансамбле термодинамич. среднее имеет вид:

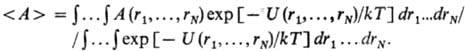
Данный метод применим практически ко всем системам; получаемые с его помощью средние величины для ограниченных объемов (N = 10²–10⁵) служат хорошим приближением для описания макроскопич. объектов и могут рассматриваться как точные результаты.

В методе мол. динамики эволюция состояния системы рассматривается с помощью численного интегрирования уравнений Ньютона для движения каждой частицы (N = = 10²–10⁵) при заданных потенциалах межчастичного взаимодействия. Равновесные характеристики системы получаются при усреднении по фазовым траекториям (по скоростям и координатам) на больших временах, после установления максвелловского распределения частиц по скоростям (т. наз. период термализации).

Ограничения в использовании численных методов в осн. определяются возможностями ЭВМ. Спец. вычислит. приемы позволяют обходить сложности, связанные с тем, что рассматривается не реальная система, а небольшой объем; это особенно важно при учете дальнодействующих потенциалов взаимод., анализе фазовых переходов и т. п.

Физическая кинетика — раздел статистич. физики, который дает обоснование соотношениям термодинамики необратимых процессов, описывающим перенос энергии, импульса и массы, а также влияние на эти процессы внеш. полей. Кинетич. коэффициенты-макроскопич. характеристики сплошной среды, определяющие зависимости потоков физ. величин (теплоты, импульса, массы компонентов и др.) от вызывающих эти потоки градиентов температуры, концентрации, гидродинамич. скорости и др. Необходимо различать коэффициенты Онсагера, входящие в уравнения, связывающие потоки с термодинамич. силами (термодинамич. уравнения движения), и коэффициенты переноса (диффузии, теплопроводности, вязкости и т. п.), входящие в уравнения переноса. Первые м. б. выражены через вторые с помощью соотношений между макроскопич. характеристиками системы, поэтому в дальнейшем будут рассматриваться лишь коэф. переноса.

Для расчета макроскопич. коэф. переноса необходимо провести усреднение по вероятностям реализаций элементарных актов переноса с помощью неравновесной функции распределения. Главная сложность заключается в том, что аналит. вид функции распределения f(р, q, т) (т-время) неизвестен (в отличие от равновесного состояния системы, которое описывается с помощью функций распределения Гиббса, получаемых при т : ,). Рассматривают n-частичные функции распределения φ_n(ρ, q, т), которые получают из функций f(р, q, т) усреднением по координатам и импульсам остальных (N — п) частиц:

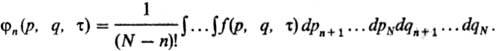
Для них м. б. составлена система уравнений, позволяющая описать произвольные неравновесные состояния. Решение этой системы уравнений очень сложно. Как правило, в кинетич. теории газов и газообразных квазичастиц в твердом теле (фермионов и бозонов) используется лишь уравнение для одно-частичной функции распределения φ₁. В предположении об отсутствии корреляции между состояниями любых частиц (гипотеза мол. хаоса) получено т. наз. кинетич. уравнение БоЛьцмана (Л. Больцман, 1872). Это уравнение учитывает изменение функции распределения частиц под действием внеш. силы F(r, т) и парных столкновений между частицами:

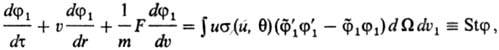
где φ₁(u, r, т) и 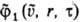-функции распределения частиц до столкновения, φ'₁(u', r, т) и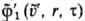-функции распределения после столкновения; u и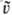-скорости частиц до столкновения, u' и 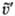-скорости тех же частиц после столкновения, и = |u —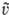|-модуль относит. скорости сталкивающихся частиц, q — угол между относит. скоростью u — 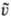сталкивающихся частиц и линией, соединяющей их центры, σ(u,q)dW-дифференц. эффективное сечение рассеяния частиц на телесный угол dW в лаб. системе координат, зависящее от закона взаимод. частиц. Для модели молекул в виде упругих жестких сфер, имеющих радиус R, принимается σ = 4R²cosq. В рамках классич. механики дифференц. сечение выражается через параметры столкновения b и ε (соотв. прицельное расстояние и азимутальный угол линии центров): σdW = bdbdε, а молекулы рассматриваются как центры сил с потенциалом, зависящим от расстояния. Для квантовых газов выражение для дифференц. эффективного сечения получают на основе квантовой механики, с учетом влияния эффектов симметрии на вероятность столкновения.

Если система находится в статистич. равновесии, интеграл столкновений Stφ равен нулю и решением кинетич. уравнения Больцмана будет распределение Максвелла. Для неравновесных состояний решения кинетич. уравнения Больцмана обычно ищут в виде разложения в ряд функции φ₁(u, r, т) по малым параметрам относительно функции распределения Максвелла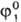. В простейшем (релаксационном) приближении интеграл столкновений аппроксимируется как Stφ = = -(φ₁ — 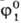)/т*, где т*-среднее время релаксации. Зная решение уравнения Больцмана, можно определить плотность числа частиц газа в точке r в момент времени т: n = = тφ₁(u, r, т)du и др. средние значения величин, характеризующих состояние газа: средняя (по абс. значениям) скорость молекул, средний квадрат их скорости и т. д., а через них рассчитать гидродинамич. характеристики процессов переноса энергии, импульса и числа частиц, которые могут в нем происходить.

Данный подход реализуется при исследовании процессов в газовых смесях, в многоатомных газах с учетом внутр. степеней свободы молекул (колебат., вращат. и т. д.), в плотных газах, при изучении влияния стенок сосудов на распределения молекул газа в приповерхностной области и мн. др. задачах. Анализ решений кинетич. уравнения Больц-мана позволяет обосновать область применимости условия локального термодинамич. равновесия и определить вклады в поток, обусловленные неравновесностью потока. Неравновесный поток импульса дает сдвиговую вязкость; для газов с внутр. степенями свободы молекул он дополнительно содержит член, обусловленный объемной вязкостью. Плотность потока энергии пропорциональна градиенту температуры (обычная теплопроводность), а в случае смеси газов она содержит член, пропорциональный градиенту концентраций (эффект Дюфура). Поток вещества в смеси газов содержит член, пропорциональный градиенту концентрации (обычная диффузия), и член, пропорциональный градиенту температуры (термодиффузия). Физ. кинетика дает для этих коэф. пропорциональности выражения через эффективные сечения столкновения, следовательно через потенциалы межмол. взаимодействий. Коэф. переноса удовлетворяют принципу симметрии, выражающему симметрию уравнений механики относительно изменения знака времени (теорема Онсагера).

Для сильно разреженных газов, когда длина своб. пробега молекулы l между двумя последоват. соударениями значительно превосходит характерный размер системы L (1/L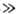1), гидродинамич. уравнения неприменимы и необходимо решать кинетич. уравнение Больцмана с определенными граничными условиями на поверхности. Эти условия определяются функцией распределения молекул, рассеянных из-за взаимод. со стенкой.

Кинетич. уравнение Больцмана для фононов кристаллич. решетки позволяет исследовать теплопроводность и поглощение звука в диэлектриках, а кинетич. уравнение Больцмана для электронов с учетом их взаимод. с фононами-электрич. сопротивление и объясняет гальваномагн., термоэлектрич., термомагн. и др. явления в металлах, а также особенности поведения сверхпроводников в высокочастотных полях.

Для описания неравновесных процессов в жидкостях од-ночастичная функция распределения φ₁ не раскрывает специфики явлений и требуется рассмотрение двухчастичной функции распределения φ₂. Однако для достаточно медленных процессов и в случаях, когда масштабы пространств. неодно-родностей значительно меньше масштаба корреляции между частицами жидкости, можно использовать локально равновесную одночастичную функцию распределения с температурой, хим. потенциалами и гидродинамич. скоростью, которые соответствуют рассматриваемому малому объему жидкости. К ней можно найти поправку, пропорциональную градиентам температуры, гидродинамич. скорости и хим. потенциалам компонентов, и вычислить потоки импульсов, энергии и вещества, а также обосновать уравнения Навье — Стокса, теплопроводности и диффузии. В этом случае коэф. переноса оказываются пропорциональными пространственно-временным корреляц. функциям потоков энергии, импульса и вещества каждого компонента.

Для описания процессов переноса вещества в твердых телах и на границах раздела с твердым телом широко используется решеточная модель конденсир. фазы. Эволюция состояния системы описывается осн. кинетич. уравнением (master equation) относительно функции распределения P(q, т):

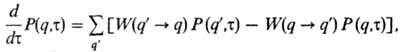
где P(q,т)= тf(p,q,т)du- функция распределения, усредненная по импульсам (скоростям) всех N частиц, описывающая распределение частиц по узлам решеточной структуры (их число равно N_y, N < N_y), q- номер узла или его координата. В модели "решеточного газа" частица может находиться в узле (узел занят) или отсутствовать (узел свободен); W(q : q')-вероятность перехода системы в единицу времени из состояния q, описываемого полным набором координат частиц, в др. состояние q'. Первая сумма описывает вклад всех процессов, в которых осуществляется переход в данное состояние q, вторая сумма-выход из этого состояния. В случае равновесного распределения частиц (т : ,) P(q) = exp[-H(q)/kT]/Q, где Q — статистич. сумма, H(q)-энергия системы в состоянии q. Вероятности перехода удовлетворяют детального равновесия принципу: W(q':q)exp[-H(q')/kT] = W(q : q') ехр[-H(q)/kТ]. На базе уравнений для функций P(q,т) строят кинетич. уравнения для n-частичных функций распределения, которые получают путем усреднения по расположениям всех остальных (N — п) частиц. Для малых η кинетич. уравнения м. б. решены аналитически или численно и с их помощью м. б. получены коэф. диффузии, самодиффузии, сдвиговой вязкости, подвижности и т. п. Такой подход применим к процессам переноса вещества в моноатомных кристаллах, сплавах, оксидных кристаллах, ионитах и т. д., к процессам переноса вещества через границу с твердым телом, роста кристаллов, фазовым превращениям и т. п. Для межфазного переноса, из-за различий в характерных временах протекания элементарных процессов миграции частиц, важную роль играет вид граничных условий на границах раздела фаз.

Для малых систем (число узлов N_y = 10² — 10⁵) система уравнений относительно функции P(q,т) м. б. решена численно методом Монте — Карло. Этап релаксации системы к равновесному состоянию позволяет рассмотреть разл. переходные процессы при исследовании кинетики фазовых превращений, роста кристаллов, кинетики поверхностных реакций и т. д. и определить их динамич. характеристики, в т. ч. и коэф. переноса.

Для расчета коэф. переноса в газообразных, жидких и твердых фазах, а также на границах раздела фаз активно используются разнообразные варианты метода мол. динамики, который позволяет детально проследить за эволюцией системы от времен ~10⁻¹⁵с до ~10⁻¹⁰с (на временах порядка 10⁻¹⁰— 10⁻⁹с и более используются т. наз. уравнения Ланжевена, это уравнения Ньютона, содержащие в правой части стохастич. слагаемое).

Для систем с хим. реакциями на характер распределения частиц большое влияние оказывает соотношение между характерными временами переноса реагентов и их хим. превращения. Если скорость хим. превращения мала, распределение частиц не сильно отличается от случая, когда реакция отсутствует. Если скорость реакции велика, ее влияние на характер распределения частиц велико и использовать средние концентрации частиц (т. е. функции распределения с n = 1), как это делается при использовании закона действующих масс, нельзя. Необходимо более детально описывать распределение реагентов с помощью функций распределения φ_n с n > 1. Важное значение при описании реакц. потоков частиц на поверхности и скоростей диффузионно-контролируемых реакций имеют граничные условия (см. макрокинетика).

^{Лит.: Кубо Р., Статистическая механика, пер. с англ., М.,1967; Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971; Исихара А., Статистическая физика, пер. с англ., М., 1973; Ландау Л. Д., Лифшиц E. М_L Статистическая физика, 3 изд., ч. 1, М., 1976; Ферцигер Дж., Капер Г., Математическая теория процессов переноса в газах, пер. с англ., М., 1976; Румер Ю. Б., Рывкин М. Ш., Термодинамика. Статистическая физика и кинетика, 2 изд., М., 1977; Смирнова H. А., Методы статистической термодинамики в физической химии, 2 изд., М., 1982; Берклеевский курс физики, пер. с англ., 3 изд., т. 5-Рейф Ф., Статистическая физика, М., 1986; Товбин Ю.К., Теория физико-химических процессов на границе газ-твердое тело, М., 1990.}

_{Ю. К. Товбин}